题目内容
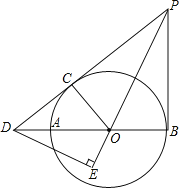
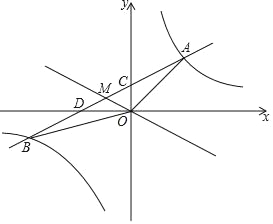
【题目】如图,一次函数y=kx+1与反比例函数y=![]() (m≠0)相交于A、B两点,与x轴,y轴分别交于D、C两点,已知sin∠CDO=
(m≠0)相交于A、B两点,与x轴,y轴分别交于D、C两点,已知sin∠CDO=![]() ,△BOD的面积为1.
,△BOD的面积为1.
(1)求一次函数和反比例函数的解析式;
(2)连接OA,OB,点M是线段AB的中点,直线OM向上平移h(h>0)个单位将△AOB的面积分成1:7两部分,求h的值.
【答案】(1)y=![]() ;(2)h=
;(2)h=![]() .
.
【解析】
(1)解直角三角形求出点D坐标,再利用三角形的面积公式求出点B坐标即可解决问题;
(2)设平移后的中交OA于G,交AC于H.利用方程组求出点A坐标,利用中点坐标公式求出点M坐标,求出直线OM的解析式,再证明S△AHG:S△AOM=1:4,推出AG:AO=1:2,推出GA=OG,可得G(1,1),求出直线GH的解析式即可解决问题;
解:(1)由题意点C(0,1),
在Rt△ODC中,∵OC=1,sin∠CDO=![]() ,
,
∴OD=2,
∴D(﹣2,0),
把D(﹣2,0)代入y=kx+1,得到k=![]() ,
,
∴一次函数的解析式为y=![]() x+1,
x+1,
∵△BOD的面积为1,设B(x,y),
∴![]() ×2×|y|=1,
×2×|y|=1,
∵y<0,
∴y=﹣1,
∴B(﹣4,﹣1),
∴m=4,
∴反比例函数的解析式为y=![]() .
.
(2)设平移后的中交OA于G,交AC于H.
由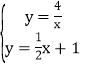 ,解得
,解得![]() 或
或![]() ,
,
∴A(2,2),∵B(﹣4,﹣1),
∴M(﹣1,![]() ),
),
∴直线OM的解析式为y=﹣![]() x,
x,
∵AM=MB,
∴S△AMO=S△BMO,
∵S△AHG:S四边形OBHG=1:7,
∴S△AHG:S△AOM=1:4,
∴AG:AO=1:2,
∴GA=OG,
∴G(1,1),
∴直线HG的解析式为y=﹣![]() x+
x+![]() ,
,
∴h=![]() .
.

【题目】光华农机租赁公司共有50台联合收割机,其中甲型20台,乙型30台,先将这50台联合收割机派往A、B两地区收割小麦,其中30台派往A地区,20台派往B地区.两地区与该农机租赁公司商定的每天的租赁价格见表:
每台甲型收割机的租金 | 每台乙型收割机的租金 | |
A地区 | 1800 | 1600 |
B地区 | 1600 | 1200 |
(1)设派往A地区x台乙型联合收割机,租赁公司这50台联合收割机一天获得的租金为y(元),求y与x间的函数关系式,并写出x的取值范围;
(2)若使农机租赁公司这50台联合收割机一天获得的租金总额不低于79 600元,说明有多少种分配方案,并将各种方案设计出来;
(3)如果要使这50台联合收割机每天获得的租金最高,请你为光华农机租赁公司提一条合理化建议.