题目内容
【题目】已知AB∥CD，点M、N分别是AB、CD上两点，点G在AB、CD之间，连接MG、NG．
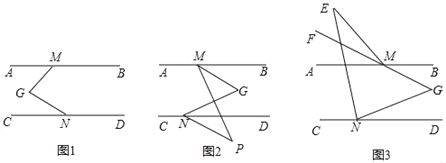
（1）如图1，若GM⊥GN，求∠AMG+∠CNG的度数；
（2）如图2，若点P是CD下方一点，MG平分∠BMP，ND平分∠GNP，已知∠BMG＝30°，求∠MGN+∠MPN的度数；
（3）如图3，若点E是AB上方一点，连接EM、EN，且GM的延长线MF平分∠AME，NE平分∠CNG，2∠MEN+∠MGN＝105°，求∠AME的度数．
【答案】（1）∠AMG+∠CNG＝90°；（2）∠MGN+∠MPN＝90°；（3）∠AME＝50°．
【解析】
（1）过G作GH∥AB，依据两直线平行，内错角相等，即可得到∠AMG+∠CNG的度数；
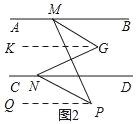
（2）过G作GK∥AB，过点P作PQ∥AB，设∠GND=α，利用平行线的性质以及角平分线的定义，求得∠MGN=30°+α，∠MPN=60°-α，即可得到∠MGN+∠MPN=30°+α+60°-α=90°；
（3）过G作GK∥AB，过E作ET∥AB，设∠AMF=x，∠GND=y，利用平行线的性质以及角平分线的定义，可得∠MEN=∠TEN-∠TEM=90°-
y-2x，∠MGN=x+y，再根据2∠MEN+∠MGN=105°，即可得到2（90°-y-2x）+x+y=105°，求得x=25°，即可得出∠AME=2x=50°．
（1）如图1，过G作GH∥AB，
∵AB∥CD，
∴GH∥AB∥CD，
∴∠AMG＝∠HGM，∠CNG＝∠HGN，
∵MG⊥NG，
∴∠MGN＝∠MGH+∠NGH＝∠AMG+∠CNG＝90°；
（2）如图2，过G作GK∥AB，过点P作PQ∥AB，设∠GND＝α，
∵GK∥AB，AB∥CD，
∴GK∥CD，
∴∠KGN＝∠GND＝α，
∵GK∥AB，∠BMG＝30°，
∴∠MGK＝∠BMG＝30°，
∵MG平分∠BMP，ND平分∠GNP，
∴∠GMP＝∠BMG＝30°，
∴∠BMP＝60°，
∵PQ∥AB，
∴∠MPQ＝∠BMP＝60°，
∵ND平分∠GNP，
∴∠DNP＝∠GND＝α，
∵AB∥CD，
∴PQ∥CD，
∴∠QPN＝∠DNP＝α，
∴∠MGN＝30°+α，∠MPN＝60°﹣α，
∴∠MGN+∠MPN＝30°+α+60°﹣α＝90°；
（3）如图3，过G作GK∥AB，过E作ET∥AB，设∠AMF＝x，∠GND＝y，
∵AB，FG交于M，MF平分∠AME，
∴∠FME＝∠FMA＝∠BMG＝x，
∴∠AME＝2x，
∵GK∥AB，
∴∠MGK＝∠BMG＝x，
∵ET∥AB，
∴∠TEM＝∠EMA＝2x，
∵CD∥AB∥KG，
∴GK∥CD，
∴∠KGN＝∠GND＝y，
∴∠MGN＝x+y，
∵∠CND＝180°，NE平分∠CNG，
∴∠CNG＝180°﹣y，∠CNE＝∠CNG＝90°﹣y，
∵ET∥AB∥CD，
∴ET∥CD，
∴∠TEN＝∠CNE＝90°﹣y，
∴∠MEN＝∠TEN﹣∠TEM＝90°﹣y﹣2x，∠MGN＝x+y，
∵2∠MEN+∠MGN＝105°，
∴2（90°﹣y﹣2x）+x+y＝105°，
∴x＝25°，
∴∠AME＝2x＝50°．
