题目内容
如图，已知正方形纸片ABCD，M，N分别是AD、BC的中点，把BC边向上翻折，使点C恰好落在MN上的P点处，BQ为折痕，则∠PBQ= 度．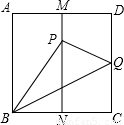
【答案】分析：根据折叠的性质知：可知：BN=
BP，从而可知∠BPN的值，再根据∠PBQ=∠CBQ，可将∠PBQ的角度求出．
解答：解：根据折叠的性质知：BP=BC，∠PBQ=∠CBQ
∴BN=
BC=
BP
∵∠BNP=90°
∴∠BPN=30°
∴∠PBQ=
×60°=30°．
故答案为30．
点评：已知折叠问题就是已知图形的全等，根据边之间的关系，可将∠PBQ的度数求出．
BP，从而可知∠BPN的值，再根据∠PBQ=∠CBQ，可将∠PBQ的角度求出．解答：解：根据折叠的性质知：BP=BC，∠PBQ=∠CBQ
∴BN=
BC=BP∵∠BNP=90°
∴∠BPN=30°
∴∠PBQ=
×60°=30°．故答案为30．
点评：已知折叠问题就是已知图形的全等，根据边之间的关系，可将∠PBQ的度数求出．
练习册系列答案
相关题目
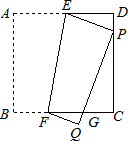与C、D不重合），折痕为EF，折叠后AB边落在PQ的位置，PQ与BC交于点G．
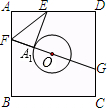如图，已知正方形纸片ABCD的边长为8，O是正方形的中心，⊙O的半径为2．沿EF折叠纸片，使点A落在⊙O上的A1处，且EA1所在直线与⊙O只有一个公共点A1，延长FA1交CD边于点G，则A1G的长是（ ）
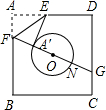如图，已知正方形纸片ABCD的边长为8，⊙0的半径为2，圆心在正方形的中心上，将纸片按图示方式折叠，使E A′恰好与⊙0相切于点A′（△EFA′与⊙0除切点外无重叠部分），延长FA′交CD边于点G，则A′G的长是
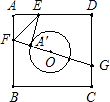如图，已知正方形纸片ABCD的边长为8，⊙O的半径为2，圆心在正方形的中心上，将纸片按图示方式折叠，使EA恰好与⊙O相切于点A′（△EFA′与⊙O除切点外无重叠部分），延长FA′交CD边于点G，求A′G的长．
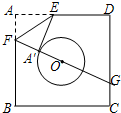如图，已知正方形纸片ABCD的边长为4，⊙O的半径为1，圆心在正方形的中心上，将纸片按图示方式折叠，使E A′恰好与⊙O相切于点A′，延长F A′交CD边于点G，则A′G的长是