题目内容
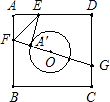如图，已知正方形纸片ABCD的边长为8，⊙O的半径为2，圆心在正方形的中心上，将纸片按图示方式折叠，使EA恰好与⊙O相切于点A′（△EFA′与⊙O除切点外无重叠部分），延长FA′交CD边于点G，求A′G的长．
分析：作FS⊥CD于点S点，由于点O是正方形的中心，正方形是中心对称图形，则AF=CG，先证明△AFE≌△FA′E，有FA=FA′；再根据四边形ADSF是矩形，设AF=A′F=DS=CG=x，利用勾股定理得[2（2+x）]2=（8-2x）2+82，解方程得x=
，所以A′G=FG-FA′=
．
| 7 |
| 3 |
| 19 |
| 3 |
解答：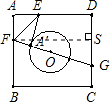
解：如图，作FS⊥CD于点S，则AF=CG，
∵△AFE≌△A′FE，
∴FA=FA′，
∵四边形ADSF是矩形，
∴AF=SD，AD=FS；
设AF=x，则A′F=DS=CG=x，GS=8-2x，FO=FA′+OA′=2+x，FG=2（2+x）；
∵FG2=GS2+FS2
∴[2（2+x）]2=（8-2x）2+82，
解得x=
，
∴A′G=FG-FA′=2（2+x）-x=
．
解：如图，作FS⊥CD于点S，则AF=CG，∵△AFE≌△A′FE，
∴FA=FA′，
∵四边形ADSF是矩形，
∴AF=SD，AD=FS；
设AF=x，则A′F=DS=CG=x，GS=8-2x，FO=FA′+OA′=2+x，FG=2（2+x）；
∵FG2=GS2+FS2
∴[2（2+x）]2=（8-2x）2+82，
解得x=
| 7 |
| 3 |
∴A′G=FG-FA′=2（2+x）-x=
| 19 |
| 3 |
点评：本题利用了正方形是中心对称图形，正方形的性质，勾股定理，折叠的性质求解．
练习册系列答案
相关题目
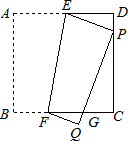与C、D不重合），折痕为EF，折叠后AB边落在PQ的位置，PQ与BC交于点G．
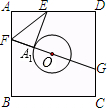如图，已知正方形纸片ABCD的边长为8，O是正方形的中心，⊙O的半径为2．沿EF折叠纸片，使点A落在⊙O上的A1处，且EA1所在直线与⊙O只有一个公共点A1，延长FA1交CD边于点G，则A1G的长是（ ）
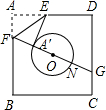如图，已知正方形纸片ABCD的边长为8，⊙0的半径为2，圆心在正方形的中心上，将纸片按图示方式折叠，使E A′恰好与⊙0相切于点A′（△EFA′与⊙0除切点外无重叠部分），延长FA′交CD边于点G，则A′G的长是
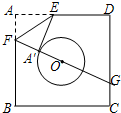如图，已知正方形纸片ABCD的边长为4，⊙O的半径为1，圆心在正方形的中心上，将纸片按图示方式折叠，使E A′恰好与⊙O相切于点A′，延长F A′交CD边于点G，则A′G的长是