题目内容
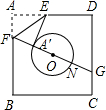 如图,已知正方形纸片ABCD的边长为8,⊙0的半径为2,圆心在正方形的中心上,将纸片按图示方式折叠,使E A′恰好与⊙0相切于点A′(△EFA′与⊙0除切点外无重叠部分),延长FA′交CD边于点G,则A′G的长是
如图,已知正方形纸片ABCD的边长为8,⊙0的半径为2,圆心在正方形的中心上,将纸片按图示方式折叠,使E A′恰好与⊙0相切于点A′(△EFA′与⊙0除切点外无重叠部分),延长FA′交CD边于点G,则A′G的长是| 19 |
| 3 |
| 19 |
| 3 |
分析:连AC,过F作FH⊥DC于H,根据折叠的性质得∠EA′F=∠EAF=90°,FA′=FA,由E A′恰好与⊙0相切于点A′,根据切线的性质得OA′⊥EA′,则点F、A′、O共线,即FG过圆心O;再根据正方形的性质得到AC经过点O,且OA=OC,易证得△OAF≌△OCG,则OF=OG,AF=CG,易得FA′=GN,设FA=x,DC=8,ON=2,则FA′=DH=CG=GN=x,FG=FA′+A′N+NG=2x+4,HG=DC-DH-CG=8-2x,在Rt△FGH中,利用勾股定理得到FG2=FH2+HG2,即(2x+4)2=82+(8-2x)2,解出x=
,则可计算出A′G=A′N+NG=4+
=
.
| 7 |
| 3 |
| 7 |
| 3 |
| 19 |
| 3 |
解答:解:连AC,过F作FH⊥DC于H,如图 .
.
∵△AEF沿EF折叠得到△A′EF,
∴∠EA′F=∠EAF=90°,FA′=FA,
∵E A′恰好与⊙0相切于点A′,
∴OA′⊥EA′,
∴点F、A′、O共线,即FG过圆心O,
又∵点O为正方形的中心,
∴AC经过点O,
∴OA=OC,
易证得△OAF≌△OCG,
∴OF=OG,AF=CG,
∵OA′=ON,
∴FA′=GN,
设FA=x,DC=8,ON=2,则FA′=DH=CG=GN=x,FG=FA′+A′N+NG=2x+4,HG=DC-DH-CG=8-2x,
在Rt△FGH中,FG2=FH2+HG2,
∴(2x+4)2=82+(8-2x)2,解得x=
,
∴A′G=A′N+NG=4+
=
.
故答案为
.
 .
.∵△AEF沿EF折叠得到△A′EF,
∴∠EA′F=∠EAF=90°,FA′=FA,
∵E A′恰好与⊙0相切于点A′,
∴OA′⊥EA′,
∴点F、A′、O共线,即FG过圆心O,
又∵点O为正方形的中心,
∴AC经过点O,
∴OA=OC,
易证得△OAF≌△OCG,
∴OF=OG,AF=CG,
∵OA′=ON,
∴FA′=GN,
设FA=x,DC=8,ON=2,则FA′=DH=CG=GN=x,FG=FA′+A′N+NG=2x+4,HG=DC-DH-CG=8-2x,
在Rt△FGH中,FG2=FH2+HG2,
∴(2x+4)2=82+(8-2x)2,解得x=
| 7 |
| 3 |
∴A′G=A′N+NG=4+
| 7 |
| 3 |
| 19 |
| 3 |
故答案为
| 19 |
| 3 |
点评:本题考查了切线的性质:圆的切线垂直于过切点的半径.也考查了折叠和正方形的性质以及勾股定理.

练习册系列答案
相关题目
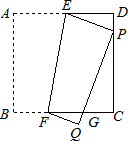 与C、D不重合),折痕为EF,折叠后AB边落在PQ的位置,PQ与BC交于点G.
与C、D不重合),折痕为EF,折叠后AB边落在PQ的位置,PQ与BC交于点G.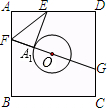 如图,已知正方形纸片ABCD的边长为8,O是正方形的中心,⊙O的半径为2.沿EF折叠纸片,使点A落在⊙O上的A1处,且EA1所在直线与⊙O只有一个公共点A1,延长FA1交CD边于点G,则A1G的长是( )
如图,已知正方形纸片ABCD的边长为8,O是正方形的中心,⊙O的半径为2.沿EF折叠纸片,使点A落在⊙O上的A1处,且EA1所在直线与⊙O只有一个公共点A1,延长FA1交CD边于点G,则A1G的长是( )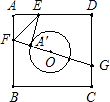 如图,已知正方形纸片ABCD的边长为8,⊙O的半径为2,圆心在正方形的中心上,将纸片按图示方式折叠,使EA恰好与⊙O相切于点A′(△EFA′与⊙O除切点外无重叠部分),延长FA′交CD边于点G,求A′G的长.
如图,已知正方形纸片ABCD的边长为8,⊙O的半径为2,圆心在正方形的中心上,将纸片按图示方式折叠,使EA恰好与⊙O相切于点A′(△EFA′与⊙O除切点外无重叠部分),延长FA′交CD边于点G,求A′G的长.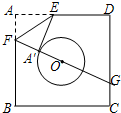 如图,已知正方形纸片ABCD的边长为4,⊙O的半径为1,圆心在正方形的中心上,将纸片按图示方式折叠,使E A′恰好与⊙O相切于点A′,延长F A′交CD边于点G,则A′G的长是
如图,已知正方形纸片ABCD的边长为4,⊙O的半径为1,圆心在正方形的中心上,将纸片按图示方式折叠,使E A′恰好与⊙O相切于点A′,延长F A′交CD边于点G,则A′G的长是