题目内容
如图,已知正方形纸片ABCD的边长为2,将正方形纸片折叠,使顶点A落在边CD上的点P处(点P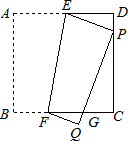 与C、D不重合),折痕为EF,折叠后AB边落在PQ的位置,PQ与BC交于点G.
与C、D不重合),折痕为EF,折叠后AB边落在PQ的位置,PQ与BC交于点G.(1)观察操作结果,找到一个与△EDP相似的三角形,并证明你的结论;
(2)当点P位于CD中点时,你找到的三角形与△EDP周长的比是多少?
分析:(1)根据题意,∠EPG=90°,可得∠EPD+∠CPG=90°,又∠EPD+∠PED=90°,所以∠CPG=∠PED.加上∠C=∠D,可得△EDP∽△PCG;
(2)根据相似三角形性质求解.因为CP=1,所以需求对应边DE的长度.设DE=x,则AE=EP=2-x,根据勾股定理可求.
(2)根据相似三角形性质求解.因为CP=1,所以需求对应边DE的长度.设DE=x,则AE=EP=2-x,根据勾股定理可求.
解答:解: (1)与△EDP相似的三角形是△PCG. (1分)
(1)与△EDP相似的三角形是△PCG. (1分)
证明:∵四边形ABCD是正方形,
∴∠A=∠C=∠D=90°.
由折叠知∠EPQ=∠A=90°.
∴∠1+∠3=90°,∠1+∠2=90°.
∴∠2=∠3.
∴△PCG∽△EDP. (2分)
(2)设ED=x,则AE=2-x,
由折叠可知:EP=AE=2-x.
∵点P是CD中点,
∴DP=1.
∵∠D=90°,
∴ED2+DP2=EP2,
即x2+12=(2-x)2
解得x=
.
∴ED=
. (3分)
∵△PCG∽△EDP,
∴
=
=
.
∴△PCG与△EDP周长的比为4:3. (4分)
 (1)与△EDP相似的三角形是△PCG. (1分)
(1)与△EDP相似的三角形是△PCG. (1分)证明:∵四边形ABCD是正方形,
∴∠A=∠C=∠D=90°.
由折叠知∠EPQ=∠A=90°.
∴∠1+∠3=90°,∠1+∠2=90°.
∴∠2=∠3.
∴△PCG∽△EDP. (2分)
(2)设ED=x,则AE=2-x,
由折叠可知:EP=AE=2-x.
∵点P是CD中点,
∴DP=1.
∵∠D=90°,
∴ED2+DP2=EP2,
即x2+12=(2-x)2
解得x=
| 3 |
| 4 |
∴ED=
| 3 |
| 4 |
∵△PCG∽△EDP,
∴
| PC |
| ED |
| 1 | ||
|
| 4 |
| 3 |
∴△PCG与△EDP周长的比为4:3. (4分)
点评:此题考查了相似三角形的判定和性质,涉及折叠问题、勾股定理等知识点,综合性较强,难度偏上.

练习册系列答案
相关题目
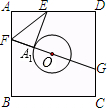 如图,已知正方形纸片ABCD的边长为8,O是正方形的中心,⊙O的半径为2.沿EF折叠纸片,使点A落在⊙O上的A1处,且EA1所在直线与⊙O只有一个公共点A1,延长FA1交CD边于点G,则A1G的长是( )
如图,已知正方形纸片ABCD的边长为8,O是正方形的中心,⊙O的半径为2.沿EF折叠纸片,使点A落在⊙O上的A1处,且EA1所在直线与⊙O只有一个公共点A1,延长FA1交CD边于点G,则A1G的长是( )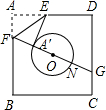 如图,已知正方形纸片ABCD的边长为8,⊙0的半径为2,圆心在正方形的中心上,将纸片按图示方式折叠,使E A′恰好与⊙0相切于点A′(△EFA′与⊙0除切点外无重叠部分),延长FA′交CD边于点G,则A′G的长是
如图,已知正方形纸片ABCD的边长为8,⊙0的半径为2,圆心在正方形的中心上,将纸片按图示方式折叠,使E A′恰好与⊙0相切于点A′(△EFA′与⊙0除切点外无重叠部分),延长FA′交CD边于点G,则A′G的长是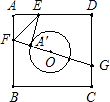 如图,已知正方形纸片ABCD的边长为8,⊙O的半径为2,圆心在正方形的中心上,将纸片按图示方式折叠,使EA恰好与⊙O相切于点A′(△EFA′与⊙O除切点外无重叠部分),延长FA′交CD边于点G,求A′G的长.
如图,已知正方形纸片ABCD的边长为8,⊙O的半径为2,圆心在正方形的中心上,将纸片按图示方式折叠,使EA恰好与⊙O相切于点A′(△EFA′与⊙O除切点外无重叠部分),延长FA′交CD边于点G,求A′G的长.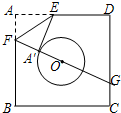 如图,已知正方形纸片ABCD的边长为4,⊙O的半径为1,圆心在正方形的中心上,将纸片按图示方式折叠,使E A′恰好与⊙O相切于点A′,延长F A′交CD边于点G,则A′G的长是
如图,已知正方形纸片ABCD的边长为4,⊙O的半径为1,圆心在正方形的中心上,将纸片按图示方式折叠,使E A′恰好与⊙O相切于点A′,延长F A′交CD边于点G,则A′G的长是