题目内容
【题目】如图,在四边形ABCD中,∠BAD=∠ADC=90°,AB=AD=4 ![]() ,CD=2
,CD=2 ![]() ,点P在四边形ABCD的边上,若点P到BD的距离为3,则点P的个数为( )
,点P在四边形ABCD的边上,若点P到BD的距离为3,则点P的个数为( ) 
A.2
B.3
C.4
D.5
【答案】A
【解析】解:过点A作AE⊥BD于E,过点C作CF⊥BD于F,∵∠BAD=∠ADC=90°,AB=AD=4 ![]() ,CD=2
,CD=2 ![]() ,
,
∴∠ABD=∠ADB=45°,
∴∠CDF=90°﹣∠ADB=45°,
∵sin∠ABD= ![]() ,
,
∴AE=ABsin∠ABD=4 ![]() sin45°=4>3,
sin45°=4>3,
CF= ![]() CD═2<3,所以在AB和AD边上有符合P到BD的距离为3的点2个,
CD═2<3,所以在AB和AD边上有符合P到BD的距离为3的点2个,
故选A.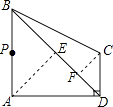
【考点精析】利用点到直线的距离和勾股定理的概念对题目进行判断即可得到答案,需要熟知从直线外一点到这条直线的垂线段的长度叫做点到直线的距离;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案【题目】“节能环保,低碳生活”是我们倡导的一种生活方式,某家电商场计划用11.8万元购进节能型电视机、洗衣机和空调共40台,三种家电的进价和售价如表所示:
价格 | 进价 | 售价 |
电视机 | 5000 | 5500 |
洗衣机 | 2000 | 2160 |
空 调 | 2400 | 2700 |
(1)在不超出现有资金的前提下,若购进电视机的数量和洗衣机的数量相同,空调的数量不超过电视机的数量的3倍.请问商场有哪几种进货方案?
(2)在“2012年消费促进月”促销活动期间,商家针对这三种节能型产品推出“现金每购1000元送50元家电消费券一张、多买多送”的活动.在(1)的条件下,若三种电器在活动期间全部售出,商家预估最多送出多少张?
【题目】个旧二中八年级9个班的全体同学参加学校第三届“青春之歌”歌咏比赛,班级的得分情况如下表:
班级(个) | 2 | 3 | 2 | 1 |
分数(分) | 92 | 94 | 96 | 97 |
那么这9个班级所得分数的众数和中位数分别是( )
A.97,92B.94,94C.94,95D.96,94
