Question

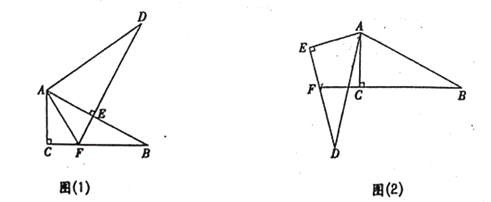
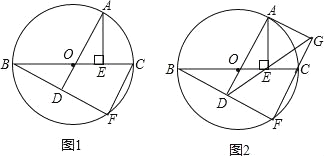
【题目】已知BC是⊙O的直径，BF是弦，AD过圆心O，AD⊥BF，AE⊥BC于E，连接FC．

（1）如图1，若OE＝2，求CF；

（2）如图2，连接DE，并延长交FC的延长线于G，连接AG，请你判断直线AG与⊙O的位置关系，并说明理由．

Answer 1

【答案】（1）4；（2）直线AG与⊙O相切.

【解析】

(1)由AAS证明△AEO≌△BDO,得出OE=OD=2,证出OD//CF,得出OD为△BFC的中位线,得出CF=2OD=4即可;

(2)由ASA证明△ABD≌△GDF,得出AD=GF,证出AD//GF,得出四边形ADFG为矩形,由矩形的性质得出AG⊥OA,即可得出结论.

解：（1）∵BC是⊙O的直径，AD过圆心O，AD⊥BF，AE⊥BC于E，

∴∠AEO＝∠BDO＝90°，OA＝OB，

在△AEO和△BDO中，

，

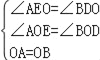∴△AEO≌△BDO（AAS），

∴OE＝OD＝2，

∵BC是⊙O的直径，

∴∠CFB＝90°，即CF⊥BF，

∴OD∥CF，

∵O为BC的中点，

∴OD为△BFC的中位线，

∴CF＝2OD＝4；

（2）直线AG与⊙O相切，理由如下：

连接AB，如图所示：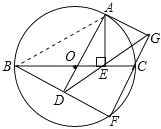

∵OA＝OB，OE＝OD，

∴△OAB与△ODE为等腰三角形，

∵∠AOB＝∠DOE，

∴∠ADG＝∠OED＝∠BAD＝∠ABO，

∵∠GDF+∠ADG＝90°＝∠BAD+∠ABD，

∴∠GDF＝∠ABD，

∵OD为△BFC的中位线，

∴BD＝DF，

在△ABD和△GDF中，

，

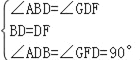∴△ABD≌△GDF（ASA），

∴AD＝GF，

∵AD⊥BF，GF⊥BF，

∴AD∥GF，

∴四边形ADFG为矩形，

∴AG⊥OA，

∴直线AG与⊙O相切．