题目内容
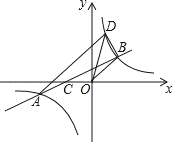
【题目】如图,点A和点B分别是反比例函数y=![]() (k≠0)图象上两点,连接AB交x轴负半轴于点C,连接BO,tan∠BCO=
(k≠0)图象上两点,连接AB交x轴负半轴于点C,连接BO,tan∠BCO=![]() ,∠BOC=135°,CO=2,过点A作AD∥BO交反比例函数y=
,∠BOC=135°,CO=2,过点A作AD∥BO交反比例函数y=![]() 于点D,连接OD,BD.
于点D,连接OD,BD.
(1)求点A的坐标;
(2)求△OBD的面积.
【答案】(1) 点A的坐标为(﹣4,﹣1).(2)3.
【解析】
(1)过点B作BE⊥x轴于点E,根据∠BOC=135°可得出∠BOE=45°,从而得出OE=BE,再根据tan∠BCO=![]() 且CO=2,可得出点B坐标为(2,2),以及反比例函数系数k的几何意义即可得出反比例函数解析式,由B、C点的坐标利用待定系数法即可求出直线AB的函数解析式,将直线AB的函数解析式代入反比例函数解析式中,得出关于x的一元二次方程,解方程即可求出点A的横坐标,将其代入反比例函数解析式中即可得出结论;
且CO=2,可得出点B坐标为(2,2),以及反比例函数系数k的几何意义即可得出反比例函数解析式,由B、C点的坐标利用待定系数法即可求出直线AB的函数解析式,将直线AB的函数解析式代入反比例函数解析式中,得出关于x的一元二次方程,解方程即可求出点A的横坐标,将其代入反比例函数解析式中即可得出结论;
(2)设直线AD与y轴交于点M,连接BM,则S△BOD=S△BOM,根据OB的解析式、AD∥OB及点A的坐标可求出直线AD的解析式,利用一次函数图象上点的坐标特征可求出点M的坐标,再利用三角形的面积公式即可求出结论.
解:(1)过点B作BE⊥x轴于点E,如图1所示.
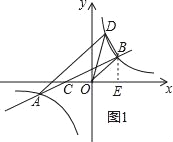
∵∠BOC=135°,
∴∠BOE=45°,
∴OE=BE.
又∵tan∠BCO=![]() =
=![]() ,OC=2,
,OC=2,
∴BE=OE=2,
∴点B的坐标为(2,2).
∴k=2×2=4,
即反比例函数的解析式为y=![]() .
.
设直线AB的解析式为y=ax+b,
将点B(2,2)、点C(﹣2,0)代入到y=ax+b中,
得![]() ,解得:
,解得: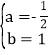 .
.
∴直线AB的解析式为y=![]() x+1.
x+1.
将y=![]() x+1代入到y=
x+1代入到y=![]() 中,
中,
得![]() =
=![]() x+1,即x2+2x﹣8=0,
x+1,即x2+2x﹣8=0,
解得:x1=﹣4,x2=2.
当x=﹣4时,y=![]() =﹣1.
=﹣1.
∴点A的坐标为(﹣4,﹣1).
(2)设直线AD与y轴交于点M,连接BM,如图2所示.
∵AD∥BO,
∴设直线AD的解析式为y=x+c,
∵点A(﹣4,﹣1)在直线AD的图象上,
∴﹣1=﹣4+c,解得:c=3.
∴直线AD的解析式为y=x+3.
当x=0时,y=x+3=3,
∴点M的坐标为(0,3).
∵AD∥BO,
∴S△BOD=S△BOM=![]() OMxB=
OMxB=![]() ×3×2=3.
×3×2=3.