题目内容
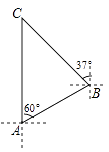
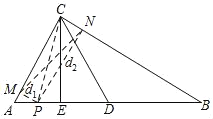
【题目】如图,点D为△ABC的AB边上的中点,点E为AD的中点,△ADC为正三角形,给出下列结论,①CB=2CE,②tan∠B=![]() ,③∠ECD=∠DCB,④若AC=2,点P是AB上一动点,点P到AC、BC边的距离分别为d1,d2,则d12+d22的最小值是3.其中正确的结论是____(填写正确结论的序号).
,③∠ECD=∠DCB,④若AC=2,点P是AB上一动点,点P到AC、BC边的距离分别为d1,d2,则d12+d22的最小值是3.其中正确的结论是____(填写正确结论的序号).
【答案】①③④
【解析】
根据中点的性质得到AD=BD,根据等边三角形的性质得到AD=CD,∠ADC=∠ACD=60°,CE⊥AB,∠DCE=30°,根据等量代换有CD=BD,根据等腰三角形的性质得到∠B=∠DCB=30°,即可判断①②③,根据勾股定理可知d12+d22=MN2=CP2,根据垂线段最短,则当CP⊥AB时,d12+d22的值最小,即可判断④.
∵D是AB中点
∴AD=BD
∵△ACD是等边三角形,E是AD中点
∴AD=CD,∠ADC=∠ACD =60°,CE⊥AB,∠DCE=30°
∴CD=BD
∴∠B=∠DCB=30°,且∠DCE=30°,CE⊥AB
∴∠ECD=∠DCB,BC=2CE,tan∠B=![]()
故①③正确,②错误
∵∠DCB=30°,∠ACD=60°
∴∠ACB=90°
若AC=2,点P是AB上一动点,点P到AC、BC边的距离分别为d1,d2,
∴四边形PMCN是矩形
∴MN=CP
∵d12+d22=MN2=CP2
∴当CP为最小值,d12+d22的值最小
∴根据垂线段最短,则当CP⊥AB时,d12+d22的值最小
此时:∠CAB=60°,AC=2,CP⊥AB
∴CP=![]() ,
,
∴d12+d22=MN2=CP2=3
即d12+d22的最小值为3
故④正确
故答案为①③④

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目