题目内容
已知:在Rt△ABC中,∠B=90°,BC=4cm,AB=8cm,D、E、F分别为AB、AC、BC边上的中点.若P为AB边上的一个动点,PQ∥BC,且交AC于点Q,以PQ为一边,在点A的异侧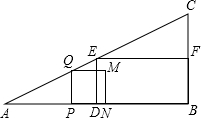 作正方形PQMN,记正方形PQMN与矩形EDBF的公共部分的面积为y.
作正方形PQMN,记正方形PQMN与矩形EDBF的公共部分的面积为y.(1)如图,当AP=3cm时,求y的值;
(2)设AP=xcm,试用含x的代数式表示y(cm2);
(3)当y=2cm2时,试确定点P的位置.
分析:(1)先根据AP的长,求出PQ的值,然后看看正方形与矩形是否重合,若重合求出重合部分的线段的长,然后根据矩形的面积计算公式进行求解即可.
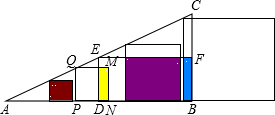
(2)要分四种情况进行讨论:
①当N在D点或D点左侧时,当正方形PQMN的边MN与矩形EDBF的边ED重合时,利用相似三角形的性质可得出x=
,即0<x≤
时,此时正方形与矩形没有重合,因此y=0;
②当N在D点右侧,而P点在D点左侧或与D点重合时,即
<x≤4,此时正方形与矩形重合的面积应该是以DN为长,NM为宽的矩形,DN=PN-PD=PN-(AD-AP)=x-(4-
x)=
x-4.而NM=PQ=
x,因此重合部分的面积应该是y=(
x-4)×
x=
x2-2x;
③当P在D点右侧,而N点在B点左侧或与B点重合时,即4<x≤
时,此时正方形重合部分的面积应该是以正方形边长为长,DE为宽的矩形的面积,PN=
x,DE=2,因此此时重合部分的面积是y=
x×2=x;
④当P在B左侧时,而N点在AB延长线上时,即
<x<8时,此时重合部分的面积应该是以DE长为宽,PA长为长的矩形的面积.BP=AB-AP=8-x,BF=DE=2,因此此时重合部分的面积应该是y=(8-x)×2=16-2x.
(3)将y=2代入(2)的式子中,看看求出的x哪个符合条件即可.
(2)要分四种情况进行讨论:
①当N在D点或D点左侧时,当正方形PQMN的边MN与矩形EDBF的边ED重合时,利用相似三角形的性质可得出x=
| 8 |
| 3 |
| 8 |
| 3 |
②当N在D点右侧,而P点在D点左侧或与D点重合时,即
| 8 |
| 3 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
③当P在D点右侧,而N点在B点左侧或与B点重合时,即4<x≤
| 16 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
④当P在B左侧时,而N点在AB延长线上时,即
| 16 |
| 3 |
(3)将y=2代入(2)的式子中,看看求出的x哪个符合条件即可.
解答:解:(1)∵在Rt△ABC中,∠B=90°,BC=4cm,AB=8cm,
∴tanA=
=
,
∵D是AB中点,
∴DE是△ABC的中位线,
∴AD=BD=4cm,DE=2cm,
∴Rt△APQ中,AP=3cm,
∴PQ=AP•tanA=3×
=1.5cm,
∴DN=AN-AD=AP+PN-AD=3+1.5-4=0.5,
∴重合部分的面积应该是y=DN×MN=1.5×0.5=0.75cm2;
(2)当0<x≤
,y=0;
当
<x≤4,y=
x2-2x,
当4<x≤
,y=x;
当
<x<8,y=16-2x;
(3)当
<x≤4时,如果y=2,2=
x2-2x,解得x=
或x=
(舍去);
当4<x≤
时,如果y=2,x=2,也不符合题意,
当
<x<8时,如果y=2,2=16-2x,解得x=7,因此当AP=7cm时,y=2cm2.
∴当x=7cm或x=
cm时,y=2cm2.
∴tanA=
| BC |
| AB |
| 1 |
| 2 |
∵D是AB中点,
∴DE是△ABC的中位线,
∴AD=BD=4cm,DE=2cm,
∴Rt△APQ中,AP=3cm,
∴PQ=AP•tanA=3×
| 1 |
| 2 |
∴DN=AN-AD=AP+PN-AD=3+1.5-4=0.5,
∴重合部分的面积应该是y=DN×MN=1.5×0.5=0.75cm2;
(2)当0<x≤
| 8 |
| 3 |
当
| 8 |
| 3 |
| 3 |
| 4 |
当4<x≤
| 16 |
| 3 |
当
| 16 |
| 3 |

(3)当
| 8 |
| 3 |
| 3 |
| 4 |
4+2
| ||
| 3 |
4-2
| ||
| 3 |
当4<x≤
| 16 |
| 3 |
当
| 16 |
| 3 |
∴当x=7cm或x=
4+2
| ||
| 3 |
点评:本题主要考查了直角三角形的性质,正方形的性质,中位线定理以及解直角三角形的应用等知识点,要注意(2)(3)中,正方形的位置不同时,函数解析式是不同的,要分类讨论,不要漏解.

练习册系列答案
相关题目
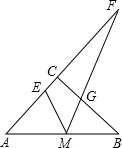 如图,已知:在Rt△ABC中,∠ACB=90°,AC=BC=4,M是边AB的中点,E、G分别是边AC、BC上的一点,∠EMG=45°,AC与MG的延长线相交于点F.
如图,已知:在Rt△ABC中,∠ACB=90°,AC=BC=4,M是边AB的中点,E、G分别是边AC、BC上的一点,∠EMG=45°,AC与MG的延长线相交于点F.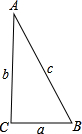 已知:在Rt△ABC中,∠C=90°,∠A=30°,b=
已知:在Rt△ABC中,∠C=90°,∠A=30°,b=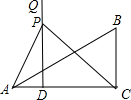 重合),过D作DQ⊥AC(DQ与AB在AC的同侧);点P从D点出发,在射线DQ上运动,连接PA、PC.
重合),过D作DQ⊥AC(DQ与AB在AC的同侧);点P从D点出发,在射线DQ上运动,连接PA、PC.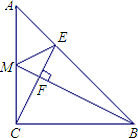 已知:在Rt△ABC中,∠C=90°,AC=BC,M是AC的中点,连接BM,CF⊥MB,F是垂足,延长CF交AB于点E.求证:∠AME=∠CMB.
已知:在Rt△ABC中,∠C=90°,AC=BC,M是AC的中点,连接BM,CF⊥MB,F是垂足,延长CF交AB于点E.求证:∠AME=∠CMB. 已知:在Rt△ABC中,∠C=90°,点O在AB上,以O为圆心,OA长为半径的圆与AC、AB分别交于点D、E,且∠CBD=∠A.
已知:在Rt△ABC中,∠C=90°,点O在AB上,以O为圆心,OA长为半径的圆与AC、AB分别交于点D、E,且∠CBD=∠A.