题目内容
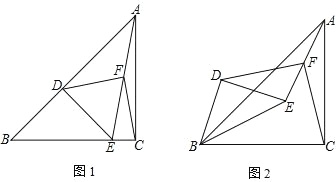
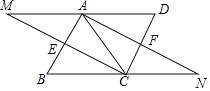
【题目】已知:如图,在平行四边形ABCD中,BC=AC,E,F分别是AB,CD的中点,连接CE并延长交DA的延长线于M,连接AF并延长交BC的延长线于N.
(1)求证:△ABN≌△CDM;
(2)当平行四边形ABCD的边或角满足什么关系时,四边形AECF是正方形?请说明理由.
【答案】(1)证明见解析;(2)当∠B=45°时,四边形AECF是正方形,理由见解析.
【解析】
(1)根据平行四边形得到AB=CD,AB∥CD,∠B=∠D,根据线段中点的定义得到AE=![]() AB,CF=
AB,CF=![]() CD,推出四边形AECF是平行四边形,得到四边形AECF是矩形,根据全等三角形的判定定理得到结论;
CD,推出四边形AECF是平行四边形,得到四边形AECF是矩形,根据全等三角形的判定定理得到结论;
(2)根据直角三角形的性质即可得到结论.
(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,∠B=∠D,
∵E,F分别是AB,CD的中点,
∴AE=![]() AB,CF=
AB,CF=![]() CD,
CD,
∴AE=CF,
∵AE∥CF,
∴四边形AECF是平行四边形,
∵AC=CB,
∴CE⊥AB,
∴∠AEC=90°,
∴四边形AECF是矩形,
∴∠BAN=∠DCM=90°,
在△ABN与△CDM中,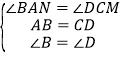 ,
,
∴△ABN≌△CDM(ASA);
(2)解:当∠B=45°时,四边形AECF是正方形,
理由:∵BC=AC,
∴∠B=∠BAC=45°,
∵E是AB的中点,
∴CE⊥AB,
∴AE=EC,
∴矩形AECF是正方形.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目