题目内容
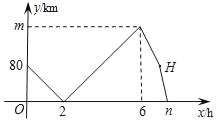
【题目】如图,直线 ![]() :
: ![]() 与直线
与直线 ![]() :
: ![]() 相交于点P(1,b)
相交于点P(1,b)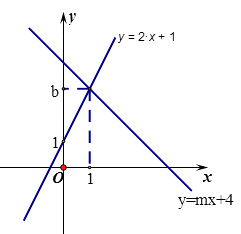
(1)求b,m的值
(2)垂直于x轴的直线 ![]() 与直线
与直线 ![]() ,
, ![]() 分别相交于C,D,若线段CD长为2,求a的值
分别相交于C,D,若线段CD长为2,求a的值
【答案】
(1)
解:把点P(1,b)代入y=2x+1,得b=2+1=3,
把点P(1,3)代入y=mx+4,得m+4=3,
∴m=-1.
(2)
解:直线x=a与直线l1的交点C为(a,2a+1),与直线l2的交点D为(a,-a+4).
∵CD=2,
∴|2a+1-(-a+4)|=2,
即|3a-3|=2,
∴3a-3=2或3a-3=-2,
∴a=![]() 或a=
或a=![]() .
.
【解析】(1)把点P(1,b)分别代入l1和l2,得到b和m的值.
(2)将直线x=a分别与直线l1、l2联立求出C和D的坐标,根据CD=2,列出关于a的方程求出a的值即可.
【考点精析】本题主要考查了确定一次函数的表达式的相关知识点,需要掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法才能正确解答此题.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
【题目】在一个不透明的袋中有除颜色外其他完全相同的3个球,每次从袋中摸出一个球,记下颜色后放回搅匀再摸,在摸球试验中得到下表中部分数据:
摸球 总次数 | 40 | 80 | 120 | 160 | 200 | 240 | 280 | 320 | 360 | 400 |
摸到黄球的次数 | 14 | 23 | 38 | 52 | 67 | 86 | 97 | 111 | 120 | 136 |
摸到黄球的频率 | 35% | 32% | 33% | 35% | 35% |
(1)请将上表补充完整(结果精确到1%);
(2)制作折线统计图表示摸到黄球的频率的变化情况;
(3)估计从袋中摸出一个球是黄球的概率是多少.