题目内容
【题目】(本题12分)如图1,在平面直角坐标系中,四边形OABC各顶点的坐标分别O(0,0),A(3, ![]() ),B(9,5
),B(9,5 ![]() ),C(14,0).动点P与Q同时从O点出发,运动时间为t秒,点P沿OC方向以1单位长度/秒的速度向点C运动,点Q沿折线OAABBC运动,在OA,AB,BC上运动的速度分别为3,
),C(14,0).动点P与Q同时从O点出发,运动时间为t秒,点P沿OC方向以1单位长度/秒的速度向点C运动,点Q沿折线OAABBC运动,在OA,AB,BC上运动的速度分别为3, ![]() ,
, ![]() (单位长度/秒)﹒当P,Q中的一点到达C点时,两点同时停止运动.
(单位长度/秒)﹒当P,Q中的一点到达C点时,两点同时停止运动.

(1)求AB所在直线的函数表达式.
(2)如图2,当点Q在AB上运动时,求△CPQ的面积S关于t的函数表达式及S的最大值.
(3)在P,Q的运动过程中,若线段PQ的垂直平分线经过四边形OABC的顶点,求相应的t值.
【答案】
(1)
解:把A(3,3 ),B(9,5 )代入y=kx+b,
得 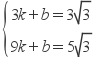 ;解得:
;解得: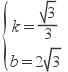 ;
;
∴y= ![]() x+2
x+2![]() ;
;
(2)
解:在△PQC中,PC=14-t,PC边上的高线长为![]() ;
;
∴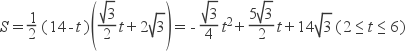
∴当t=5时,S有最大值;最大值为![]() .
.
(3)
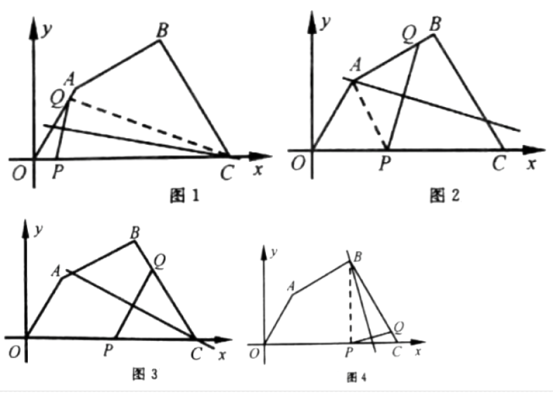
解: a.当0<t≤2时,线段PQ的中垂线经过点C(如图1);
可得方程![]()
解得:![]() ,
,![]() (舍去),此时t=
(舍去),此时t=![]() .
.
b.当2<t≤6时,线段PQ的中垂线经过点A(如图2)
可得方程![]() ,
,
解得:![]() ;
;![]() (舍去),此时
(舍去),此时![]() ;
;
c.当6<t≤10时,
①线段PQ的中垂线经过点C(如图3)
可得方程14-t=25-![]() ;
;
解得:t=![]() .
.
②线段PQ的中垂线经过点B(如图4)
可得方程![]() ;
;
解得![]() ,
,![]() (舍去);
(舍去);
此时![]() ;
;
综上所述:t的值为![]() ,
,![]() ,
,![]() ,
,![]() .
.
【解析】(1)用待定系数法求直线AB方程即可。
(2)根据三角形的面积公式得到关于t的二次三项式,再由二次函数图像的性质求出S的最大值即可。
(3)根据t的值分情况讨论,依题意列出不同的方程从而求出t的值。
【考点精析】利用确定一次函数的表达式和二次函数的最值对题目进行判断即可得到答案,需要熟知确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法;如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a.