题目内容
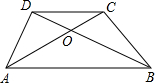已知如图，梯形ABCD中，AB∥CD，△COD与△AOB的周长比为1：2，则CD：AB=________，
S△COB：S△COD=________．
1：2 2：1
分析：先证明△COD与△AOB相似，再根据相似三角形周长的比等于相似比，CD：AB就是△COD与△AOB的相似比；△COB，△COD是等高三角形，所以面积的比等于底边BO与OD的比．
解答：∵AB∥CD，
∴△COD∽△AOB，
∵△COD与△AOB的周长比为1：2，
∴CD：AB=1：2；
∵△COB，△COD是等高三角形，
又BO：OD=AB：CD=2：1，
∴S△COB：S△COD=BO：OD=2：1．
故应填：1：2；2：1．
点评：本题主要考查相似三角形周长的比等于相似比的性质和等高的三角形的面积的比等于底边的比的性质，需要熟练掌握并灵活运用．
分析：先证明△COD与△AOB相似，再根据相似三角形周长的比等于相似比，CD：AB就是△COD与△AOB的相似比；△COB，△COD是等高三角形，所以面积的比等于底边BO与OD的比．
解答：∵AB∥CD，
∴△COD∽△AOB，
∵△COD与△AOB的周长比为1：2，
∴CD：AB=1：2；
∵△COB，△COD是等高三角形，
又BO：OD=AB：CD=2：1，
∴S△COB：S△COD=BO：OD=2：1．
故应填：1：2；2：1．
点评：本题主要考查相似三角形周长的比等于相似比的性质和等高的三角形的面积的比等于底边的比的性质，需要熟练掌握并灵活运用．
练习册系列答案
优加精卷系列答案
相关题目
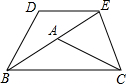（2012•通州区一模）已知如图，在△ABC中，AB=AC，∠ABC=α，将△ABC以点B为中心，沿逆时针方向旋转α度（0°＜α＜90°），得到△BDE，点B、A、E恰好在同一条直线上，连接CE．
.
S梯形ABCD ?若存在,请求出该点坐标,若不存在,请说明理由.
，请你求出四边形DBCE的面积.
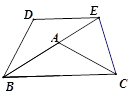
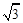，请你求出四边形DBCE的面积.
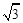，请你求出四边形DBCE的面积.