题目内容
【题目】如图，平行四边形ABCD中，AB=2，AD=4，对角线AC，BD相交于点O，且E，F，G，H分别是AO，BO，CO，DO的中点，则下列说法正确的是（ ）
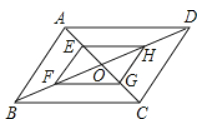
A.EH=HGB.四边形EFGH是平行四边形
C.AC⊥BDD.
的面积是
的面积的2倍
【答案】B
【解析】
根据三角形中位线的性质和平行四边形的性质分别判断各选项即可解答，
解：因为E、H为OA、OD的中点，
所以，EH＝
＝2，同理，HG＝
＝1，所以，A错误；
EH∥AD，EH＝，
FG∥BC，FG＝
，
因为平行四边形ABCD中，AD＝BC，且AD∥BC，
所以，EH＝FG，且EH∥FG，
所以，四边形EFGH是平行四边形， B正确．
AC与BD不一定垂直，C错误；
由相似三角形的面积比等于相似比的平方，知：△ABC的面积是△EFO的面积的4倍，D错误；
故选B.
练习册系列答案
挑战100单元检测试卷系列答案
相关题目
