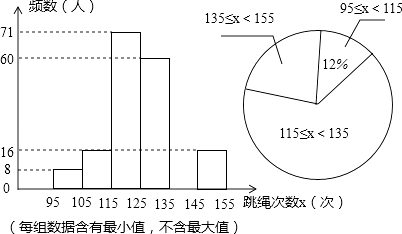
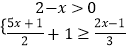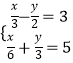题目内容
【题目】如图,在直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a、b、c满足关系式 ![]()
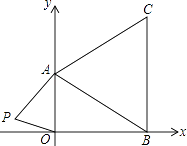
(1)求a、b、c的值;
(2)如果在第二象限内有一点P(m, ![]() ),请用含m的式子表示四边形ABOP的面积;
),请用含m的式子表示四边形ABOP的面积;
(3)在(2)的条件下,是否存在点P,使四边形ABOP的面积为△ABC的面积相等?若存在,求出点P的坐标;若不存在,请说明理由.
【答案】
(1)解:由已知 ![]() ,可得:a=2,b=3,c=4
,可得:a=2,b=3,c=4
(2)解:∵S△ABO= ![]() ×2×3=3,S△APO=
×2×3=3,S△APO= ![]() ×2×(﹣m)=﹣m,
×2×(﹣m)=﹣m,
∴S四边形ABOP=S△ABO+S△APO=3+(﹣m)=3﹣m,即S四边形ABOP=3﹣m
(3)解:因为S△ABC= ![]() ×4×3=6,
×4×3=6,
∵S四边形ABOP=S△ABC
∴3﹣m=6,
则 m=﹣3,
所以存在点P(﹣3, ![]() )使S四边形ABOP=S△ABC
)使S四边形ABOP=S△ABC
【解析】根据绝对值、平方数、被开方数的非负性得到a=2,b=3,c=4;根据三角形的面积求出S四边形ABOP=S△ABO+S△APO=3+(﹣m)=3﹣m,即S四边形ABOP=3﹣m;由三角形ABC的面积为6,S四边形ABOP=S△ABC,3﹣m=6,求出 m=﹣3,所以存在点P 使S四边形ABOP=S△ABC.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目