题目内容
【题目】在我市开展的“阳光体育”跳绳活动中,为了了解中学生跳绳活动的开展情况,随机抽查了全市八年级部分同学1分钟跳绳的次数,将抽查结果进行统计,并绘制两个不完整的统计图.请根据图中提供的信息,解答下列问题: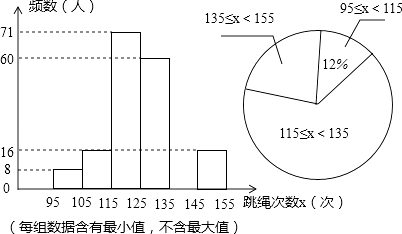
(1)本次共抽查了多少名学生?
(2)请补全频数分布直方图空缺部分,直接写出扇形统计图中跳绳次数范围135≤x<155所在扇形的圆心角度数.
(3)若本次抽查中,跳绳次数在125次以上(含125次)为优秀,请你估计全市8000名八年级学生中有多少名学生的成绩为优秀?
(4)请你根据以上信息,对我市开展的学生跳绳活动谈谈自己的看法或建议.
【答案】
(1)解:抽查的总人数:(8+16)÷12%=200(人)
(2)解:范围是135≤x<145的人数是:200﹣8﹣16﹣71﹣60﹣16=29(人),
则跳绳次数范围135≤x<155所在扇形的圆心角度数是:360× ![]() =81°.
=81°.
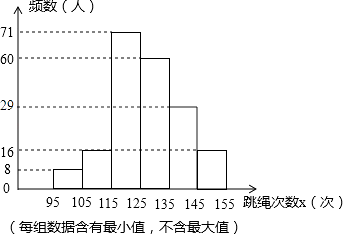
(3)解:优秀的比例是: ![]() ×100%=52.5%,
×100%=52.5%,
则估计全市8000名八年级学生中有多少名学生的成绩为优秀人数是:8000×52.5%=4200(人)
(4)解:全市达到优秀的人数有一半以上,反映了我市学生锻炼情况很好
【解析】①根据统计图得到抽查的总人数:(8+16)÷12%=200(人);②根据范围是135≤x<145的人数是:200﹣8﹣16﹣71﹣60﹣16=29(人),则跳绳次数范围135≤x<155所在扇形的圆心角度数是81°;③根据优秀的比例是:(60+29+16)÷200=0.525=52.5%,则估计全市8000名八年级学生中有多少名学生的成绩为优秀人数是:8000×52.5%=4200(人);④全市达到优秀的人数有一半以上,反映了我市学生锻炼情况很好.
【考点精析】通过灵活运用频数分布直方图和扇形统计图,掌握特点:①易于显示各组的频数分布情况;②易于显示各组的频数差别.(注意区分条形统计图与频数分布直方图);能清楚地表示出各部分在总体中所占的百分比.但是不能清楚地表示出每个项目的具体数目以及事物的变化情况即可以解答此题.

 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案