��Ŀ����
��ͼ��һ�κ���y��kx��3��ͼ��ֱ�x�ᡢy���ڵ�C����D���뷴�������� ��ͼ���ڵ��������ཻ�ڵ�P������PA��x���ڵ�A��PB��y���ڵ�B����֪B��0����6����S��DBP��27.
��ͼ���ڵ��������ཻ�ڵ�P������PA��x���ڵ�A��PB��y���ڵ�B����֪B��0����6����S��DBP��27.
��1��������һ�κ����뷴���������ı���ʽ��
��2�����Q��һ�κ���y��kx��3ͼ���ϵ�һ�㣬�������DOQ������ǡ�COD�����2����ֱ��д����Q������.
��3�������������� ��ͼ�����ABP���й����㣬ֱ��д��n��ȡֵ��Χ.
��ͼ�����ABP���й����㣬ֱ��д��n��ȡֵ��Χ.

 ��ͼ���ڵ��������ཻ�ڵ�P������PA��x���ڵ�A��PB��y���ڵ�B����֪B��0����6����S��DBP��27.
��ͼ���ڵ��������ཻ�ڵ�P������PA��x���ڵ�A��PB��y���ڵ�B����֪B��0����6����S��DBP��27.��1��������һ�κ����뷴���������ı���ʽ��
��2�����Q��һ�κ���y��kx��3ͼ���ϵ�һ�㣬�������DOQ������ǡ�COD�����2����ֱ��д����Q������.
��3��������������
 ��ͼ�����ABP���й����㣬ֱ��д��n��ȡֵ��Χ.
��ͼ�����ABP���й����㣬ֱ��д��n��ȡֵ��Χ.
��1��y=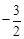 x+3��
x+3��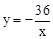 ����2����-4��9����4��-3������3��-36��n��0��
����2����-4��9����4��-3������3��-36��n��0��
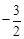 x+3��
x+3��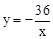 ����2����-4��9����4��-3������3��-36��n��0��
����2����-4��9����4��-3������3��-36��n��0�������������1������������������BP���ó�P�����꣬���뺯���Ľ���ʽ�������.
��2������������QM�����ɵó�Q�ĺ����꣬�������Q�������꼴��.
��3������P��A��B�����꼴�ɵó��𰸣�
��1����һ�κ���y=kx+3��ͼ��y���ڵ�D����OD=3.
��B��0��-6������BD=3+6=9.
��S��DBP=27�����������������ʽ�ã�BP="6." ��P��������ǣ�6��-6��.
��P���������y=kx+3�ã�
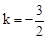 .
.һ�κ����Ľ���ʽ��y=
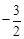 x+3.
x+3.��P���������
 �ã�m=-36.
�ã�m=-36.�෴���������Ľ���ʽ��
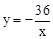 .
.��2����һ�κ���y=
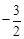 x+3.��ͼ��x���ڵ�C��
x+3.��ͼ��x���ڵ�C�����y=0�������x=2����C�������ǣ�2��0����OC=2.
��Ϊ�����������Q������DC��ʱ����Q��QM��y����M��
�ߡ�DOQ������ǡ�COD�����2����
����ݵȸߵ������ε�����ȵ��ڶ�Ӧ�ı�֮�ȵã�DQ=2DC��
�ߡ�DOC�ס�DMQ��
��
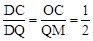 ����MQ=2OC=4.
����MQ=2OC=4.��x=4����y=
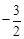 x+3�ã�y=-3������ʱQ�������ǣ�4��-3��.
x+3�ã�y=-3������ʱQ�������ǣ�4��-3��.��Q������CD��ʱ��ͬ�����QM=4��
��x=-4����y=
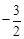 x+3�ã�y=-3������ʱQ�������ǣ�-4��9��.
x+3�ã�y=-3������ʱQ�������ǣ�-4��9��.��Q�������ǣ�-4��9����4��-3��.
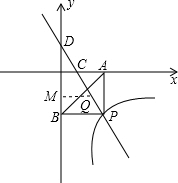
��3����A��6��0����B��0��-6����P��6��-6��������������
 ��ͼ�����ABP���й����㣬
��ͼ�����ABP���й����㣬�൱����������ͼ���P��ʱ�����n=-36.
��n��ȡֵ��Χ��-36��n��0��

��ϰ��ϵ�д�
�����Ŀ
 ����
���� ����
���� ����
���� ����
���� �����У���һ�κ������У� ��
�����У���һ�κ������У� �� ,
, ,
, ,������ͼ��ʾ�ķ�ʽ����,��
,������ͼ��ʾ�ķ�ʽ����,�� �͵�
�͵� �ֱ���ֱ��
�ֱ���ֱ�� ��
�� ����,��֪��
����,��֪�� ����
���� �������� .
�������� . 
 x+8��x�ᣬy��ֱ��ڵ�A��B��M��OB�ϵ�һ�㣬������ABM��AM�۵�����Bǡ������x���ϵĵ�B�䴦����ֱ��AM�Ľ���ʽΪ�� ����
x+8��x�ᣬy��ֱ��ڵ�A��B��M��OB�ϵ�һ�㣬������ABM��AM�۵�����Bǡ������x���ϵĵ�B�䴦����ֱ��AM�Ľ���ʽΪ�� ����

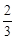 x��b�뷴��������y=
x��b�뷴��������y= �У�x��y�Ķ�Ӧֵ���±���
�У�x��y�Ķ�Ӧֵ���±���

 ��������ĺ���ֵΪ��������.
��������ĺ���ֵΪ��������.