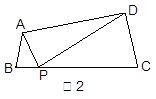题目内容
有一块直角三角形木板如图所示,已知∠C=90°,BC=3cm, AC=4cm.根据需要,要把它加工成一个正方形木板,小明和小丽分别设计了如图1和图2的两种方法,哪一块正方形木板面积更大?请说明理由.

方案二的面积大。这时正方形的边长是 cm
cm
 cm
cm解:由勾股定理得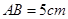 .....................2分
.....................2分
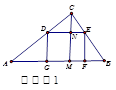
方案一:如图1作CM⊥AB于M,交DE于N
设正方形的边长为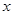 cm
cm
S△ABC=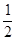 AC﹒BC=
AC﹒BC=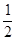 AB﹒CM得CM=
AB﹒CM得CM=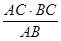 =
=
∵DE∥AB,∴△CDE∽△CAB,即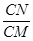 =
=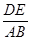
∴ ,∴
,∴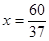 ………………………………………….5分
………………………………………….5分
方案二:如备用图(2)设正方形的边长为 cm
cm

∵EF∥AC, ∴△BFE∽△BAC, ∴
即
∴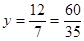 ………………………………………………………..10分
………………………………………………………..10分
∵ ,∴方案二的面积大。这时正方形的边长是
,∴方案二的面积大。这时正方形的边长是 cm
cm ………………12分
………………12分
方案一:根据题意画出图形,作CM⊥AB于M,交DE于N.设正方形边长为xcm,再根据直角三角形的面积得出CM的长,利用相似三角形的判定定理即可得出△CDE∽△CAB,再根据相似三角形的对应边成比例即可求出正方形的边长;
方案二:如图(2)设正方形边长为ycm,利用相似三角形的判定定理即可得出△BFE∽△BCA,再根据相似三角形的对应边成比例即可求出正方形的边长;把两方案中正方形的边长进行比较即可得出结论.
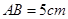 .....................2分
.....................2分方案一:如图1作CM⊥AB于M,交DE于N

设正方形的边长为
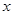 cm
cmS△ABC=
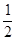 AC﹒BC=
AC﹒BC=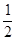 AB﹒CM得CM=
AB﹒CM得CM=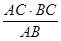 =
=
∵DE∥AB,∴△CDE∽△CAB,即
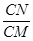 =
=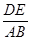
∴
 ,∴
,∴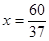 ………………………………………….5分
………………………………………….5分方案二:如备用图(2)设正方形的边长为
 cm
cm
∵EF∥AC, ∴△BFE∽△BAC, ∴

即

∴
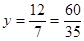 ………………………………………………………..10分
………………………………………………………..10分 ∵
 ,∴方案二的面积大。这时正方形的边长是
,∴方案二的面积大。这时正方形的边长是 cm
cm ………………12分
………………12分方案一:根据题意画出图形,作CM⊥AB于M,交DE于N.设正方形边长为xcm,再根据直角三角形的面积得出CM的长,利用相似三角形的判定定理即可得出△CDE∽△CAB,再根据相似三角形的对应边成比例即可求出正方形的边长;
方案二:如图(2)设正方形边长为ycm,利用相似三角形的判定定理即可得出△BFE∽△BCA,再根据相似三角形的对应边成比例即可求出正方形的边长;把两方案中正方形的边长进行比较即可得出结论.

练习册系列答案
相关题目
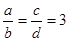 ,求
,求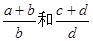 的值;
的值;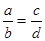 ,那么
,那么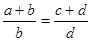 成立吗?为什么?
成立吗?为什么?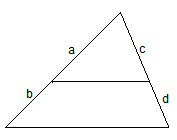
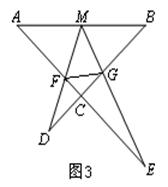
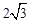 ,则四边形MABN的面积是【 】
,则四边形MABN的面积是【 】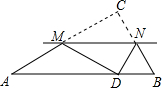



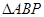 ∽
∽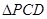 ,从而得到
,从而得到 ,解答下列问题.
,解答下列问题.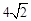 ,AF=3,求FG的长.
,AF=3,求FG的长.