题目内容
(2004•上海模拟)如图,点E在正方形ABCD的边AB上,AE=1,BE=2.点F在边BC的延长线上,且CF=BC;P是边BC上的动点(与点B不重合),PQ⊥EF,垂足为O,并交边AD于点Q;QH⊥BC,垂足为H.(1)求证:△QPH∽△FEB;
(2)设BP=x,EQ=y,求y关于x的函数解析式,并写出它的定义域;
(3)试探索△PEQ是否可能成为等腰三角形?如果可能,请求出x的值;如果不可能,请说明理由.

【答案】分析:(1)欲证△QPH∽△FEB,通过相似三角形的判断证明∠F=∠PQH,∠QHP=∠B=90°即可;
(2)求y关于x的函数解析式,可以转化到Rt△AEQ中,求出BP与AQ的关系,根据勾股定理得出;
(3)探索△PEQ是否可能成为等腰三角形,根据等腰三角形的判定分别列出函数关系式,求出x的值.
解答:证明:(1)∵PQ⊥EF,
∴∠F=90°-∠QPH,(1分)
∵QH⊥BC,
∴∠PQH=90°-∠QPH,
∴∠F=∠PQH,(1分)
∵在正方形ABCD中,∠B=90°,
∴∠QHP=∠B=90°,
∴△QPH∽△FEB.(1分)
(2)解:∵△QPH∽△FEB,
∴ ,(1分)
,(1分)
又∵QH=AB=BC=CF,
∴PH= EB=1,(1分)
EB=1,(1分)
∴AQ=BH=BP+PH=x+1,(1分)
在Rt△AEQ中,y=EQ= =
= ,(1分)
,(1分)
∴函数解析式为 ,其定义域为0<x≤2.(1分)
,其定义域为0<x≤2.(1分)
(3)解:△PEQ可能成为等腰三角形,
∵PH=1,HQ=AB=3,
∴PQ= ,
,
∵BE=2,BP=x,
∴EP= (1分),
(1分),
(1)当x满足 =
= 且0<x≤2时,EP=EQ,解得x=1;(1分)
且0<x≤2时,EP=EQ,解得x=1;(1分)
(2)当x满足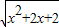 =
= 且0<x≤2时,EQ=PQ,解得x=2;(1分)
且0<x≤2时,EQ=PQ,解得x=2;(1分)
(3)当x满足 =
= 且0<x≤2时,EP=PQ.
且0<x≤2时,EP=PQ.
解方程得 ,
,
∵ ,不合题意,舍去,(1分)
,不合题意,舍去,(1分)
综上所述,当x=1或x=2时,△PEQ能成为等腰三角形.
点评:解答本题要充分利用正方形的特殊性质,相似三角形的判定,等腰三角形的判定,勾股定理与函数的结合运用.
(2)求y关于x的函数解析式,可以转化到Rt△AEQ中,求出BP与AQ的关系,根据勾股定理得出;
(3)探索△PEQ是否可能成为等腰三角形,根据等腰三角形的判定分别列出函数关系式,求出x的值.
解答:证明:(1)∵PQ⊥EF,
∴∠F=90°-∠QPH,(1分)
∵QH⊥BC,
∴∠PQH=90°-∠QPH,
∴∠F=∠PQH,(1分)
∵在正方形ABCD中,∠B=90°,
∴∠QHP=∠B=90°,
∴△QPH∽△FEB.(1分)
(2)解:∵△QPH∽△FEB,
∴
 ,(1分)
,(1分)又∵QH=AB=BC=CF,
∴PH=
 EB=1,(1分)
EB=1,(1分)∴AQ=BH=BP+PH=x+1,(1分)
在Rt△AEQ中,y=EQ=
 =
= ,(1分)
,(1分)∴函数解析式为
 ,其定义域为0<x≤2.(1分)
,其定义域为0<x≤2.(1分)(3)解:△PEQ可能成为等腰三角形,
∵PH=1,HQ=AB=3,
∴PQ=
 ,
,∵BE=2,BP=x,
∴EP=
 (1分),
(1分),(1)当x满足
 =
= 且0<x≤2时,EP=EQ,解得x=1;(1分)
且0<x≤2时,EP=EQ,解得x=1;(1分)(2)当x满足
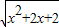 =
= 且0<x≤2时,EQ=PQ,解得x=2;(1分)
且0<x≤2时,EQ=PQ,解得x=2;(1分)(3)当x满足
 =
= 且0<x≤2时,EP=PQ.
且0<x≤2时,EP=PQ.解方程得
 ,
,∵
 ,不合题意,舍去,(1分)
,不合题意,舍去,(1分)综上所述,当x=1或x=2时,△PEQ能成为等腰三角形.
点评:解答本题要充分利用正方形的特殊性质,相似三角形的判定,等腰三角形的判定,勾股定理与函数的结合运用.

练习册系列答案
相关题目
 的图象上,求k的值.
的图象上,求k的值. ,BC=10,求AB的长.
,BC=10,求AB的长.