题目内容
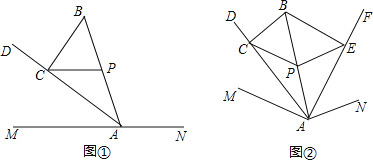
【题目】探究:如图①,点A在直线MN上,点B在直线MN外,连结AB,过线段AB的中点P作PC∥MN,交∠MAB的平分线AD于点C,连结BC,求证:BC⊥AD.
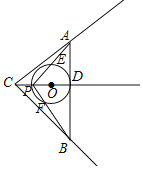
应用:如图②,点B在∠MAN内部,连结AB,过线段AB的中点P作PC∥AM,交∠MAB的平分线AD于点C;作PE∥AN,交∠NAB的平分线AF于点E,连结BC、BE.若∠MAN=150°,则∠CBE的大小为______度.
【答案】探究:证明见解析;应用:150.
【解析】
探究:根据角平分线的定义和平行线的性质得出∠PCA=∠PAC,根据等角对等边得出PC=PA,再得出PC=PB,利用三角形的内角和证明即可;
应用:根据探究中的证明得出∠BAC+∠BAE+∠CBA+∠ABE=180°,再由角平分线得出∠BAC+∠BAE=75°,最后得出答案即可.
解:探究:∵PC∥MN,
∴∠PCA=∠MAC.
∵AD为∠MAB的平分线,
∴∠MAC=∠PAC.
∴∠PCA=∠PAC,
∴PC=PA.
∵PA=PB,
∴PC=PB,
∴∠B=∠BCP.
∵∠B+∠BCP+∠PCA+∠PAC=180°,
∴∠BCA=90°,
∴BC⊥AD;
应用:∵∠MAB的平分线AD,∠NAB的平分线AF,∠MAN=150°,
∴∠BAC+∠BAE=75°,
由探究得:∠BAC+∠BAE+∠CBA+∠ABE=180°,
∴∠CBE=∠CBA+∠ABE=180°﹣75°=105°
故答案为:105.

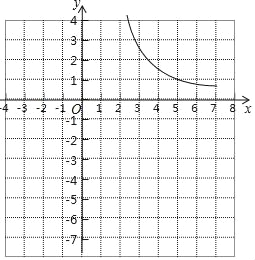
【题目】小邱同学根据学习函数的经验,研究函数y=![]() 的图象与性质.通过分析,该函数y与自变量x的几组对应值如下表,并画出了部分函数图象如图所示.
的图象与性质.通过分析,该函数y与自变量x的几组对应值如下表,并画出了部分函数图象如图所示.
x | 1 |
|
|
| 3 | 4 | 5 | 6 | … |
y | ﹣1 | ﹣2 | ﹣3.4 | ﹣7.5 | 2.4 | 1.4 | 1 | 0.8 | … |
(1)函数y=![]() 的自变量x的取值范围是 ;
的自变量x的取值范围是 ;
(2)在图中补全当1≤x<2的函数图象;
(3)观察图象,写出该函数的一条性质: ;
(4)若关于x的方程![]() =x+b有两个不相等的实数根,结合图象,可知实数b的取值范围是 .
=x+b有两个不相等的实数根,结合图象,可知实数b的取值范围是 .