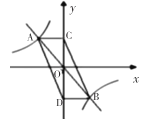
题目内容
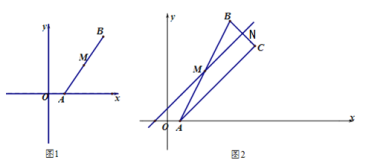
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,
,![]() ,点
,点![]() 的坐标是
的坐标是![]() .
.
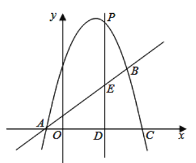
(1)如图1,求直线![]() 的解析式;
的解析式;
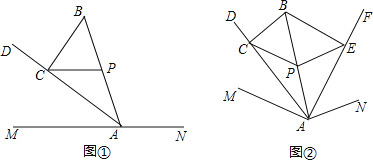
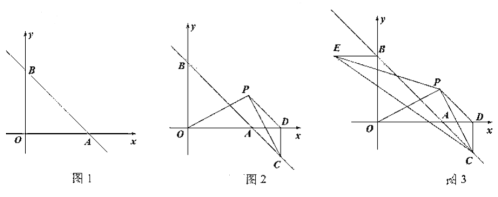
(2)如图2,点![]() 在第一象限内,连接
在第一象限内,连接![]() ,过点
,过点![]() 作
作![]() 交
交![]() 延长线于点
延长线于点![]() ,且
,且![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,连接
,连接![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,
,![]() 的而积为S,求S与
的而积为S,求S与![]() 的函数关系式(不要求写出自变量
的函数关系式(不要求写出自变量![]() 的取值范围);
的取值范围);
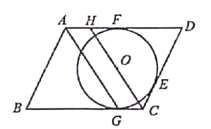
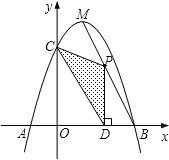
(3)如图3,在(2)的条件下,过点![]() 作
作![]() 轴,连接
轴,连接![]() 、
、![]() ,若
,若![]() ,
,![]() 时,求
时,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)求出点B的坐标,设直线![]() 解析式为
解析式为![]() ,代入A、B即可求得直线
,代入A、B即可求得直线![]() 解析式;
解析式;
(2)过点![]() 作
作![]() 于点
于点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,通过证明
,通过证明![]() ≌
≌![]() ,可得
,可得![]() ,
,![]() ,故点
,故点![]() 的横坐标为
的横坐标为![]() ,
,![]() ,设
,设![]() ,可求得
,可求得![]() ,故S与
,故S与![]() 的函数关系式为
的函数关系式为![]() ;
;
(3)延长![]() 、
、![]() 交于点
交于点![]() ,过点
,过点![]() 作
作![]() 点
点![]() ,连接
,连接![]() 、
、![]() ,先证明
,先证明![]() ≌
≌![]() ,可得
,可得![]() ,通过等量代换可得
,通过等量代换可得![]() ,再由勾股定理可得
,再由勾股定理可得![]() ,结合
,结合![]() 即可解得
即可解得![]() .
.
(1)∵![]()
∴![]() ,
,![]()
∴![]()
∴点![]()
设直线![]() 解析式为
解析式为![]()
![]()
解得![]() ,
,![]()
∴直线![]() 解析式为
解析式为![]()
(2)过点![]() 作
作![]() 于点
于点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,
,
∵![]() 轴,
轴,![]() 轴
轴
∴![]()
∴![]()
∴四边形![]() 是矩形,
是矩形,![]()
∴![]() ,
,![]()
∴![]() ,
,![]()
∴![]() ≌
≌![]()
∴![]() ,
,![]() ,点
,点![]() 的横坐标为
的横坐标为![]() ,
,![]() ,设
,设![]() ,则
,则![]() ,
,
∵![]()
∴![]()
∴![]()
∴![]()
![]()
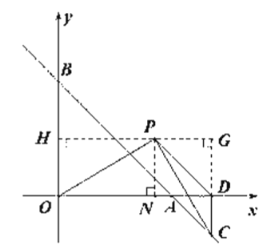
(3)延长![]() 、
、![]() 交于点
交于点![]() ,过点
,过点![]() 作
作![]() 点
点![]() ,连接
,连接![]() 、
、![]()
由(2)可知![]() ,
,![]()
∴![]()
又∵![]()
∵![]()
∴![]()
∴![]() ,
,![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,
,
∵![]() ,
,![]()
∴![]()
∵![]()
∴![]() ,
,![]() ,
,![]()
∴![]() ≌
≌![]()
∴![]()
∵![]()
∴![]()
∴![]()
∴![]()
∵![]()
∴![]()
∵![]()
∴![]()
由勾股定理可得![]()
∵![]()
∴![]() ,
,![]()
∴![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目