题目内容
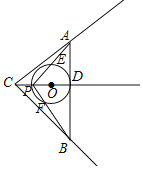
【题目】如图，在△ABC中，AB＝7，BC＝4
，∠ABC＝45°，射线CD⊥AB于D，点P为射线CD上一动点，以PD为直径的⊙O交PA、PB分别为E、F，设CP＝x．
（1）求sin∠ACD的值．
（2）在点P的整个运动过程中：
①当⊙O与射线CA相切时，求出所有满足条件时x的值；
②当x为何值时，四边形DEPF为矩形，并求出矩形DEPF的面积．
（3）如果将△ADC绕点D顺时针旋转150°，得△A′DC′，若点A′和点C′有且只有一个点在圆内，则x的取值范围是 ．
【答案】（1）sin∠ACD＝
；（2）①x的值为x＝1或x＝10；②当x＝4±2
时，四边形DEPF为矩形，矩形DEPF的面积为
；（3）
＜x＜7
【解析】
（1）如图，在Rt△BCD中，BC＝4
，∠ABC＝45°计算BD、CD，AD的长度，然后利用勾股定理求出AC的长度即可求解；
（2）①⊙O与射线CA相切包括P在AB两侧两种情况，当P在AB左侧时，如图，sin∠ACD＝
＝，而CD＝x+2r＝4，可求x，同理当P在AB右侧时可解；
②设圆的半径为r，四边形DEPF为矩形，包括P在AB两侧两种情况，当P在AB右侧时，如图设：PD＝x﹣4＝a，利用三角形APD的面积：ED＝
、DF＝
，利用ED2＝DF2可以求解，同理当当P在AB左侧的情况；
（3）利用勾股定理分别求出PA′2，PC2，然后分r2＝PA′2和 r2＝PC′2两种情况，分别求解即可．
解：（1）在Rt△BCD中，BC＝4，∠ABC＝45°，
则CD＝4，BD＝4，
,
∴AD＝AB﹣BD＝3，
sin∠ACD＝
＝；
（2）①⊙O与射线CA相切，包括P在AB两侧两种情况，
当P在AB左侧时，如下图，圆的半径为r，圆与AC相切于点H，
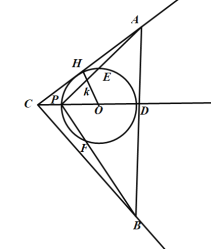
则在Rt△CHO中，OC＝x+r，OH＝r，sin∠ACD＝，
sin∠ACD＝＝，而CD＝x+2r＝4，
解得：x＝1，
同理当P在AB右侧时，求得x＝4+6＝10，
所有满足条件时x的值为x＝1或x＝10；
②设圆的半径为r，四边形DEPF为矩形，包括P在AB两侧两种情况，
当P在AB右侧时，原图的简图如下图，设∠ABP＝∠DPE＝α，
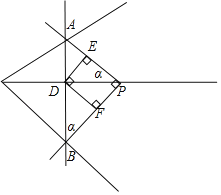
设：PD＝x﹣4＝a，
在Rt△ADP中，利用三角形APD的面积＝
EDAP＝APPD，
解得：ED＝，
同理可得：DF＝，PF2＝a2﹣DF2，
四边形DEPF为矩形，
∴ED2＝DF2，
解得：a＝2，x＝4+2，
则sinα＝
，cosα＝
，
S四边形DEPF＝DPsinαcosα＝，
同理当当P在AB左侧时，
此时PD＝4﹣x＝a，
经计算a＝2，x＝4﹣2，
S四边形DEPF＝DPsinαcosα＝，
答：当x＝4±2时，四边形DEPF为矩形，矩形DEPF的面积为；
（3）如下图，连接PA′、PC′，
在△PDA′中，AD′＝3，PD＝4﹣x，∠PDA＝150°，
利用勾股定理得：PA′2＝（
）2+（
﹣x）2＝x2﹣11x+
，
当r2＝PA′2时，解得：x＝7，
同理可得：PC2＝32+16﹣（8+4）x+x2，
当r2＝PC′2时，解得：x＝，
∴x的取值范围为：＜x＜7．
