题目内容
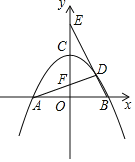
【题目】如图,抛物线y=﹣![]() x2﹣x+4与x轴交于A,B两点(A在B的左侧),与y轴交于点C.
x2﹣x+4与x轴交于A,B两点(A在B的左侧),与y轴交于点C.
(1)求点A,点B的坐标;
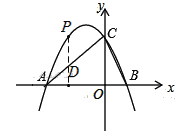
(2)P为第二象限抛物线上的一个动点,求△ACP面积的最大值.
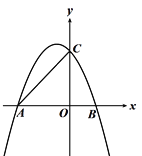
【答案】(1) A(﹣4,0),B(2,0);(2)△ACP最大面积是4.
【解析】
(1)令y=0,得到关于x 的一元二次方程﹣![]() x2﹣x+4=0,解此方程即可求得结果;
x2﹣x+4=0,解此方程即可求得结果;
(2)先求出直线AC解析式,再作PD⊥AO交AC于D,设P(t,﹣![]() t2﹣t+4),可表示出D点坐标,于是线段PD可用含t的代数式表示,所以S△ACP=
t2﹣t+4),可表示出D点坐标,于是线段PD可用含t的代数式表示,所以S△ACP=![]() PD×OA=
PD×OA=![]() PD×4=2PD,可得S△ACP关于t 的函数关系式,继而可求出△ACP面积的最大值.
PD×4=2PD,可得S△ACP关于t 的函数关系式,继而可求出△ACP面积的最大值.
(1)解:设y=0,则0=﹣![]() x2﹣x+4
x2﹣x+4
∴x1=﹣4,x2=2
∴A(﹣4,0),B(2,0)
(2)作PD⊥AO交AC于D
设AC解析式y=kx+b
∴![]()
解得:![]()
∴AC解析式为y=x+4.
设P(t,﹣![]() t2﹣t+4)则D(t,t+4)
t2﹣t+4)则D(t,t+4)
∴PD=(﹣![]() t2﹣t+4)﹣(t+4)=﹣
t2﹣t+4)﹣(t+4)=﹣![]() t2﹣2t=﹣
t2﹣2t=﹣![]() (t+2)2+2
(t+2)2+2
∴S△ACP=![]() PD×4=﹣(t+2)2+4
PD×4=﹣(t+2)2+4
∴当t=﹣2时,△ACP最大面积4.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目