题目内容
【题目】如图,扇形OAB中,∠AOB=90°.P为弧AB上的一点,过点P作PC⊥OA,垂足为C,PC与AB交于点D.若PD=2,CD=1,则该扇形的半径长为__________.
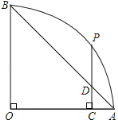
【答案】5
【解析】
连接OP,利用等腰三角形的性质可得出∠OAB=45°,结合PC⊥OA可得出△ACD为等腰直角三角形,进而可得出AC=1,设该扇形的半径长为r,则OC=r1,在Rt△POC中,利用勾股定理可得出关于r的方程,解之即可得出结论.
解:连接OP,如图所示.
∵OA=OB,∠AOB=90°,
∴∠OAB=45°,
∵PC⊥OA,
∴△ACD为等腰直角三角形,
∴AC=CD=1.
设该扇形的半径长为r,则OC=r1,
在Rt△POC中,∠PCO=90°,PC=PD+CD=3,
∴OP2=OC2+PC2,即r2=(r1)2+9,
解得:r=5.
故答案为:5.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目