题目内容
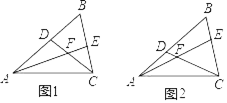
【题目】如图,在射线AB上顺次取两点C,D,使AC=CD=1,以CD为边作矩形CDEF,DE=2,将射线AB绕点A沿逆时针方向旋转,旋转角记为α(其中0°<α<45°),旋转后记作射线AB′,射线AB′分别交矩形CDEF的边CF,DE于点G,H.若CG=x,EH=y,则下列函数图象中,能反映y与x之间关系的是( )
A.
B.
C.
D.
【答案】D
【解析】∵四边形CDEF是矩形,
∴CF∥DE,
∴△ACG∽△ADH,
∴ ![]() ,
,
∵AC=CD=1,∴AD=2,
∴ ![]() ,∴DH=2x,
,∴DH=2x,
∵DE=2,∴y=2﹣2x,
∵0°<α<45°,∴0<x<1,
故答案为:D.
根据矩形的性质得出CF∥DE,可证得△ACG∽△ADH,再根据相似三角形的性质得出对应边成比例,求出DH=2x,从而可得出y与x的函数解析式,再根据0°<α<45°,求出自变量x的取值范围,即可得出选项。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】二次函数y=ax2+bx+c (a、b、c为常数且a≠0)中的x与y的部分对应值如下表,
x | … | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | … |
y | … | 12 | 5 | 0 | -3 | -4 | -3 | 0 | 5 | 12 | … |
下列四个结论:
①二次函数y=ax2+bx+c 有最小值,最小值为-3;
②抛物线与y轴交点为(0,-3);
③二次函数y=ax2+bx+c 的图像对称轴是x=1;
④本题条件下,一元二次方程ax2+bx+c的解是x1=-1,x2=3.
其中正确结论的个数是( )
A.4
B.3
C.2
D.1