题目内容
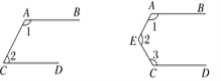
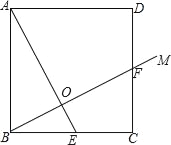
【题目】已知:正方形ABCD,E是BC的中点,连接AE,过点B作射线BM交正方形的一边于点F,交AE于点O.
(1)若BF⊥AE,
①求证:BF=AE;
②连接OD,确定OD与AB的数量关系,并证明;
(2)若正方形的边长为4,且BF=AE,求BO的长.
【答案】(1)①见解析;②OD=AB.证明见解析;(2)①BO=![]() 或BO=
或BO=![]() .
.
【解析】
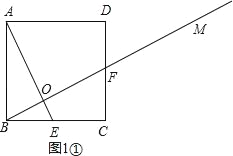
(1)①如图1①,要证BF=AE,只需证△ABE≌△BCF,只需证到∠BAE=∠CBF即可;
②延长AD,交射线BM于点G,如图1②,由△ABE≌△BCF可得BE=CF,由此可得CF=DF,从而可证到△DGF≌△CBF,则有DG=BC,从而可得DG=AD,然后运用直角三角形斜边上的中线等于斜边的一半即可解决问题;
(2)可分点F在CD上和点F在AD上两种情况进行讨论.当点F在CD上时,如图2①,易证Rt△ABE≌Rt△BCF(HL),则有∠BAE=∠CBF,由此可证到∠AOB=90°,然后在Rt△ABE中,运用面积法就可求出BO的长;当点F在AD上时,如图2②,易证Rt△ABE≌Rt△BAF(HL),则有∠BAE=∠ABF,根据等角对等边可得OB=OA,根据等角的余角相等可得∠AEB=∠EBF,根据等角对等边可得OB=OE,即可得到OA=OB=OE,只需求出AE的长就可解决问题.
(1)①如图1①,
∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠ABE=∠C=90°,
∴∠BAE+∠AEB=90°,
∵BF⊥AE,
∴∠CBF+∠AEB=90°,
∴∠BAE=∠CBF,
在△ABE和△BCF中,
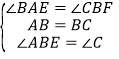 ,
,
∴△ABE≌△BCF(ASA),
∴BF=AE;
②OD=AB.
证明:延长AD,交射线BM于点G,如图1②,
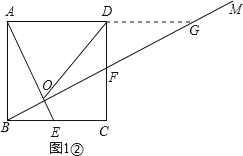
∵△ABE≌△BCF,
∴BE=CF.
∵E为BC的中点,
∴CF=BE=![]() BC=
BC=![]() DC,
DC,
∴CF=DF.
∵DG∥BC,
∴∠DGF=∠CBF.
在△DGF和△CBF中,
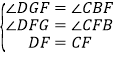 ,
,
∴△DGF≌△CBF,
∴DG=BC,
∴DG=AD.
∵BF⊥AE,
∴OD=![]() AG=AD=AB;
AG=AD=AB;
(2)①若点F在CD上,如图2①,

在Rt△ABE和Rt△BCF中,
![]() ,
,
∴Rt△ABE≌Rt△BCF(HL),
∴∠BAE=∠CBF,
∵∠BAE+∠AEB=90°,
∴∠CBF+∠AEB=90°,
∴∠AOB=90°.
∵∠ABE=90°,AB=4,BE=2,
∴AE=![]() =2
=2![]() .
.
∵S△ABE=![]() ABBE=
ABBE=![]() AEBO,
AEBO,
∴BO=![]() .
.
②若点F在AD上,如图2②,
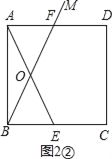
在Rt△ABE和Rt△BAF中,
![]() ,
,
∴Rt△ABE≌Rt△BAF(HL),
∴∠BAE=∠ABF,
∴OB=OA.
∵∠BAE+∠AEB=90°,∠ABF+∠EBF=90°,
∴∠AEB=∠EBF,
∴OB=OE,
∴OA=OB=OE.
∵∠ABE=90°,AB=4,BE=2,
∴AE=![]() =2
=2![]() ,
,
∴OB=![]() AE=
AE=![]() .
.
综上所述:BO的长为![]() 或
或![]() .
.

 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案【题目】已知△A1B1C1是由△ABC经过平移得到的,其中,A、B、C三点的对应点分别是A1、B1、C1,它们在平面直角坐标系中的坐标如下表所示:
△ABC | A(a,0) | B(3,0) | C(5,5) |
△A1B1C1 | A1(﹣3,2) | B1(﹣1,b) | C1(c,7) |
(1)观察表中各对应点坐标的变化,并填空:a= ,b= ,c= ;
(2)在如图的平面直角坐标系中画出△ABC及△A1B1C1;
(3)△A1B1C1的面积是 .