题目内容
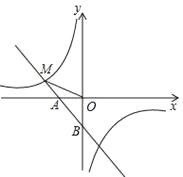
【题目】如图,在平面直角坐标系中,![]() 两点的坐标分别是点
两点的坐标分别是点![]() ,点
,点![]() ,且
,且![]() 满足:
满足:![]() .
.
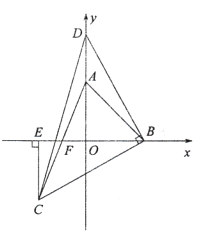
(1)求![]() 的度数;
的度数;
(2)点![]() 是
是![]() 轴正半轴上
轴正半轴上![]() 点上方一点(不与
点上方一点(不与![]() 点重合),以
点重合),以![]() 为腰作等腰
为腰作等腰![]() ,
,![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() .
.
①求证:![]() ;
;
②连接![]() 交
交![]() 轴于点
轴于点![]() ,若
,若![]() ,求点
,求点![]() 的坐标.
的坐标.
【答案】(1)45°;(2)①见解析;②(﹣2,0).
【解析】
(1)先根据非负数的性质求得a、b的值,进而可得OA、OB的长,进一步即可求出结果;
(2)①根据余角的性质可得∠ODB=∠CBE,然后即可根据AAS证得结论;
②根据全等三角形的性质和(1)的结论可得BO=CE以及OE的长,然后即可根据AAS证明△AOF≌△CEF,从而可得OF=EF,进而可得结果.
解:(1)∵![]() ,即
,即![]() ,
,
∴a-5=0,b-5=0,∴a=5,b=5,∴AO=BO=5,
∵∠AOB=90°,∴∠ABO=∠BAO=45°;
(2)①证明:∵![]() ,∴∠DBO+∠CBE=90°,
,∴∠DBO+∠CBE=90°,
∵∠ODB+∠DBO=90°,∴∠ODB=∠CBE,
∵∠BOD=∠CEB=90°,BD=CB,
∴![]() (AAS);
(AAS);
②∵![]() ,∴DO=BE,BO=CE,
,∴DO=BE,BO=CE,
∵AO=BO=5,AD=4,∴OE=AD=4,CE=5,
∵∠AOF=∠CEF,∠AFO=∠CFE,AO=CE=5,
∴△AOF≌△CEF(AAS),∴OF=EF,
∵OE=4,∴OF=2,∴点F的坐标是(﹣2,0).

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目