题目内容
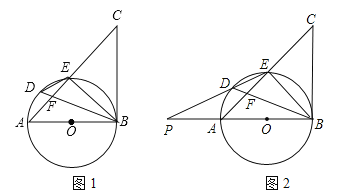
【题目】如图,在△ABO中,OA=OB,C是边AB的中点,以O为圆心的圆过点C,连接OC,AO延长线交⊙O于点D,OF是∠DOB的平分线,E为OF上一点,连接BE.
(1)求证:AB与⊙O相切;
(2)①当∠OEB=_____时,四边形OCBE为矩形;
②在①的条件下,若AB=4,则OA=_____时,四边形OCBE为正方形?
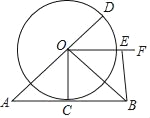
【答案】 90° ![]()
【解析】试题分析:(1)根据等腰三角形的三线合一得到OC⊥AB,根据切线的判定定理证明;
(2)①根据角平分线的定义、等腰三角形的性质得到OF∥BC,根据平行线的性质解答;
②根据邻边相等的矩形是正方形计算.
试题解析:(1)证明:∵OA=OB,C是边AB的中点,∴OC⊥AB,∴AB与⊙O相切;
(2)解:①当∠OEB=90°时,四边形OCBE为矩形,证明如下:
∵OA=OB,∴∠A=∠OBA.∵OF是∠DOB的平分线,∴∠DOF=∠BOF,由三角形的外角的性质可知,∠DOF+∠BOF=∠A+∠OBA,∴∠BOF=∠OBA,∴OF∥BC,当∠OEB=90°时,∠CBE=90°,又OC⊥AB,∴四边形OCBE为矩形.故答案为:90°;
②当OA=2![]() 时,四边形OCBE为正方形,证明如下:
时,四边形OCBE为正方形,证明如下:
∵四边形OCBE为正方形,∴CO=CB,∴OA=OB=![]() =2
=2![]() .故答案为:2
.故答案为:2![]() .
.

练习册系列答案
相关题目