题目内容
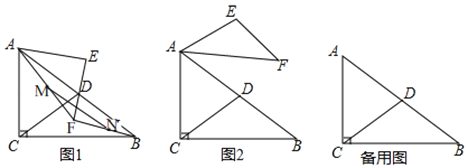
【题目】在Rt△ABC中,∠ACB=90°,AC=BC,CD为AB边上的中线.在Rt△AEF中,∠AEF=90°,AE=EF,AF<AC.连接BF,M,N分别为线段AF,BF的中点,连接MN.
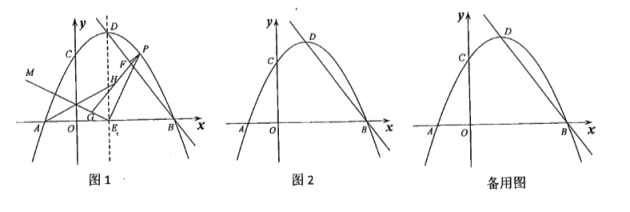
(1)如图1,点F在△ABC内,求证:CD=MN;
(2)如图2,点F在△ABC外,依题意补全图2,连接CN,EN,判断CN与EN的数量关系与位置关系,并加以证明;
(3)将图1中的△AEF绕点A旋转,若AC=a,AF=b(b<a),直接写出EN的最大值与最小值.
【答案】(1)证明见解析;(2)CN与EN的数量关系CN=EN,CN与EN的位置关系CN⊥EN.证明见解析;(3)EN的最大值为![]() ,最小值为
,最小值为![]() .
.
【解析】
(1)利用直角三角形的斜边的中线等于斜边的一半和三角形的中位线解题即可;
(2)构造出△EMN≌△DNC进而利用互余即可得出结论;
(3)借助(2)的结论,先判断出点N是以点D为圆心,![]() 为半径的圆上,即可得出答案.
为半径的圆上,即可得出答案.
解:(1)证明:在Rt△ABC中,
∵CD是斜边AB上的中线.
∴![]() .
.
在△ABF中,点M,N分别是边AF,BF的中点,
∴![]() ,
,
∴CD=MN.
(2)答:CN与EN的数量关系CN=EN,
CN与EN的位置关系CN⊥EN.
证明:连接EM,DN,如图.
与(1)同理可得 CD=MN,EM=DN.
在Rt△ABC中,CD是斜边AB边上的中线,
∴CD⊥AB.
在△ABF中,同理可证EM⊥AF.
∴∠EMF=∠CDB=90°.
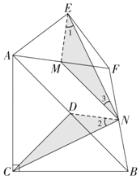
∵D,M,N分别为边AB,AF,BF的中点,
∴DN∥AF,MN∥AB.
∴∠FMN=∠MND,∠BDN=∠MND.
∴∠FMN=∠BDN.
∴∠EMF+∠FMN=∠CDB+∠BCN.
∴∠EMN=∠NDC.
∴△EMN≌△DNC.
∴CN=EN,∠1=∠2.
∵∠1+∠3+∠EMN=180°,
∴∠2+∠3+∠FMN=90°.
∴∠2+∠3+∠DNM=90°,
即∠CNE=90°.
∴CN⊥EN.
(3)点N是以点D为圆心,![]() 为半径的圆上,
为半径的圆上,
在Rt△ABC中,AC=BC=a,
∴![]() ,
,
∵CD为AB边上的中线.
∴![]() ,
,
∴CN最大=![]() ,CN最小=
,CN最小=![]()
由(2)知,EN=CN,
∴EN最大=![]() ,EN最小=
,EN最小=![]()
即:EN的最大值为![]() ,最小值为
,最小值为![]() .
.

 阅读快车系列答案
阅读快车系列答案