题目内容
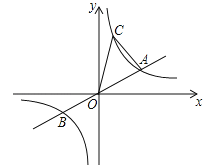
【题目】平面直角坐标系 xOy 中,抛物线 y = kx 2 - 2k 2 x -3 交 y 轴于 A 点,交直线 x=-4 于 B 点.
(1)抛物线的对称轴为直线 x=______(用含 k 的代数式表示);
(2)若 AB // x 轴,求抛物线的解析式;
(3)当-4<k<0时,记抛物线在 A,B 之间的部分为图象 G(包含 A,B 两点),若对于图象 G 上任意一点 P( xP , yP ), yP ≥-3 ,结合函数图象写出 k 的取值范围.
【答案】(1)x=k;(2)![]() (3)
(3)![]()
【解析】
(1)根据抛物线的对称轴为直线![]() 代入数据即可得出结论;
代入数据即可得出结论;
(2)由AB∥x轴,可得出点B的坐标,进而可得出抛物线的对称轴为x=2,结合(1)可得出k=-2,将其代入抛物线表达式中即可;
(3)依照题意画出函数图象,利用数形结合即可得出k的取值范围.
(1)抛物线的对称轴为![]()
故答案为:k.
(2)当x=0时,![]()
∴点![]()
∵AB∥x轴,且点B在直线![]() 上,
上,
∴点![]() ,抛物线的对称轴为直线
,抛物线的对称轴为直线![]() ,
,
∴![]()
∴抛物线的表达式为![]() .
.
(3) 当-4<k<0时,如图,
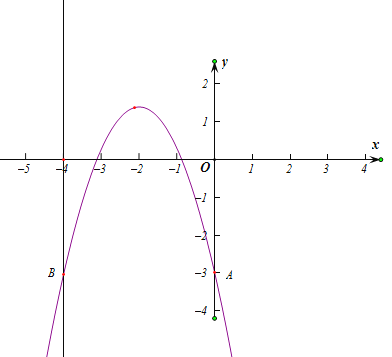
∴要使![]() 时,始终满足
时,始终满足![]() ,只需使抛物线
,只需使抛物线![]() 的对称轴与直线
的对称轴与直线![]() 重合或在直线
重合或在直线![]() 的左侧.
的左侧.
∴![]()
综上所述,![]() 的取值范围为
的取值范围为![]()

练习册系列答案
相关题目
【题目】甲、乙两名队员参加设计训练,成绩分别被制成下列两个统计图:
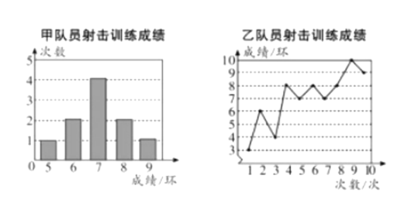
根据以上信息,整理分析数据如下:
平均数(环) | 中位数(环) | 众数(环) | 方差 | |
甲 |
|
|
|
|
乙 |
|
|
|
|
(1)表格中![]() ,
,![]() ,
,![]() ;
;
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩,若选派其中一名参赛,你认为应选哪名队员?
(3)如果乙再射击![]() 次,命中
次,命中![]() 环,那么乙的射击成绩的方差 .(填“变大”“变小”或“不变”)
环,那么乙的射击成绩的方差 .(填“变大”“变小”或“不变”)