题目内容
【题目】如图,![]() 为圆
为圆![]() 的直径,点
的直径,点![]() 在线段
在线段![]() 的延长线上,
的延长线上,![]() ,动点
,动点![]() 在圆
在圆![]() 的上半圆上运动(包含
的上半圆上运动(包含![]() 、
、![]() 两点),以线段
两点),以线段![]() 为边向上作等边三角形
为边向上作等边三角形![]() ,
,
![]() 当线段
当线段![]() 所在的直线与圆
所在的直线与圆![]() 相切时,求阴影部分的面积(图
相切时,求阴影部分的面积(图![]() )
)
![]() 设
设![]() ,当线段
,当线段![]() 与圆
与圆![]() 只有一个公共点(即
只有一个公共点(即![]() 点)时,求
点)时,求![]() 的范围(图
的范围(图![]() )
)
【答案】(1)![]() ;
;![]() 当线段
当线段![]() 与圆
与圆![]() 只有一个公共点(即
只有一个公共点(即![]() 点)时,
点)时,![]() .
.
【解析】
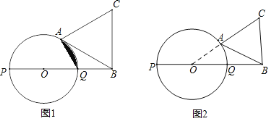
(1)连结OA,如图1,由切线的性质得OA⊥BA,而OQ=BQ=1,于是根据直角三角形斜边上的中线性质得到AQ=OQ=BQ=1,所以△OAQ为等边三角形,得到∠AOQ=60°,然后根据扇形面积公式,利用S阴影部分=S扇形AOQ﹣S△AOQ进行计算;
(2)如图2,当点A在Q点时,易α=0°,当点A为切点,由(1)得α=60°,于是可判断线段AB与圆O只有一个公共点(即A点)时,0≤α≤60°.
(1)连结OA,如图1.
∵线段AB所在的直线与圆O相切,∴OA⊥BA.
∵OQ=BQ=1,∴AQ=OQ=BQ=1,∴△OAQ为等边三角形,∴∠AOQ=60°,∴S阴影部分=S扇形AOQ﹣S△AOQ=![]() ﹣
﹣![]() ×12=
×12=![]() π﹣
π﹣![]() ;
;
(2)如图2,当点A在Q点时,α=0°,当点A为线段AB的所在的直线与⊙O相切时切点,由(1)得α=60°,所以当线段AB与圆O只有一个公共点(即A点)时,0≤α≤60°.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目