��Ŀ����
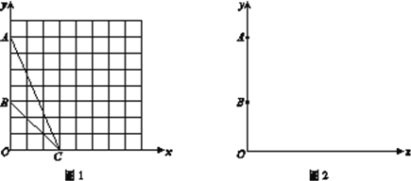
����Ŀ����֪����ͼ���ڡ�ABC�У���B=90�㣬��A=30�㣬BC=5cm������Rt��DEF�У���FDE=![]() ��DE=3cm������D��Eʼ���ڱ�AB�ϣ�����D��A����AC�����ƶ���
��DE=3cm������D��Eʼ���ڱ�AB�ϣ�����D��A����AC�����ƶ���
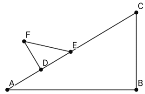
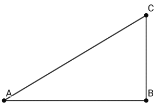
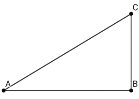
��1����Rt��DEF��AC�����ƶ��Ĺ����У�F��C����֮��ľ�����_______��������䡰���С����
��2����F��C������ABƽ��ʱ����AD�ij���
��3�����߶�AD��FC��BC�ij���Ϊ���߳�����������ֱ��������ʱ����AD�ij�
���𰸡���1����С����2��![]() ;��3��AD=6.7cm��4.2cm.
;��3��AD=6.7cm��4.2cm.
��������
��1�����������֪��DF=3cm��DC��С���ٸ��ݹ��ɶ��������жϣ�
��2������30�����Ե�ֱ�DZ���б�ߵ�һ���ƽ���ߵ����ʣ��ɵã�AC=2BC=10cm����FCD=��A=30�㣬�ٸ���������Ǻ������CD���Ӷ����AD��
��3����AD=x�����������֪��0��x��10��3=7����CD= AC��AD=10��x���ٸ��ݹ��ɶ����ɵã�FC=![]() ��Ȼ�����ֱ��������б�ߵ�����������ۣ�������ù��ɶ����ֱ����ÿ�������x��ֵ����.
��Ȼ�����ֱ��������б�ߵ�����������ۣ�������ù��ɶ����ֱ����ÿ�������x��ֵ����.
�⣺��1�����������֪��DF=DE=3cm��DC��С��
���ݹ��ɶ����ɵã�FC=![]()
��F��C����֮��ľ�����С��
�ʴ�Ϊ����С��
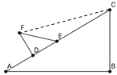
��2������ͼ��ʾ��FC��AB
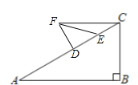
�ߡ�B=90�㣬��A=30�㣬BC=5cm��
��AC=2BC=10cm����FCD=��A=30��
��Rt��CFD��CD=![]() cm
cm
��AD=AC��CD=![]() ��
��
��3����AD=x�����������֪��0��x��10��3=7����CD= AC��AD=10��x
���ݹ��ɶ����ɵã�FC=![]()
����ADΪб��ʱ��
��AD2=FC2+BC2
��![]()
��ã�![]() ��
��
����FCΪб��ʱ��
��FC2= AD2 +BC2
��![]()
��ã�![]() ��
��
����BCΪб��ʱ��
��BC2= AD2 + FC2
��![]()
�����ã�![]()
��![]()
��˷�����.
����������AD=6.7cm��4.2cm.