题目内容
【题目】如图,四边形ABCD中,AD∥BC,DE平分∠ADB,∠BDC=∠BCD.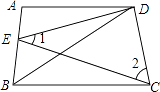
(1)求证:∠1+∠2=90°;
(2)若∠ABD的平分线与CD的延长线交于F,且∠F=55°,求∠ABC;
(3)若H是BC上一动点,F是BA延长线上一点,FH交BD于M,FG平分∠BFH,交DE于N,交BC于G.当H在BC上运动时(不与B点重合), ![]() 的值是否变化?如果变化,说明理由;如果不变,试求出其值.
的值是否变化?如果变化,说明理由;如果不变,试求出其值.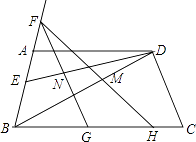
【答案】
(1)
证明:AD∥BC,
∠ADC+∠BCD=180,
∵DE平分∠ADB,
∠BDC=∠BCD,
∴∠ADE=∠EDB,
∠BDC=∠BCD,
∵∠ADC+∠BCD=180°,
∴∠EDB+∠BDC=90°,
∠1+∠2=90°
(2)
解:∠FBD+∠BDE=90°﹣∠F=35°,
∵DE平分∠ADB,BF平分∠ABD,
∴∠ADB+∠ABD=2(∠FBD+∠BDE)=70°,
又∵四边形ABCD中,AD∥BC,
∴∠DBC=∠ADB,
∴∠ABC=∠ABD+∠DBC=∠ABD+∠ADB,
即∠ABC=70°
(3)
解: ![]() 的值不变.
的值不变.
证明:在△BMF中,
∠BMF=∠DMH=180°﹣∠ABD﹣∠BFH,
又∵∠BAD=180°﹣(∠ABD+∠ADB),
∠DMH+∠BAD=(180°﹣∠ABD﹣∠BFH)+(180°﹣∠ABD﹣∠ADB),
=360°﹣∠BFH﹣2∠ABD﹣∠ADB,
∠DNG=∠FNE=180°﹣ ![]() ∠BFH﹣∠AED,
∠BFH﹣∠AED,
=180°﹣ ![]() ∠BFH﹣∠ABD﹣
∠BFH﹣∠ABD﹣ ![]() ∠ADB,
∠ADB,
= ![]() (∠DMH+∠BAD),
(∠DMH+∠BAD),
∴ ![]() =2
=2
【解析】本题考查了等腰三角形的性质、角平分线的性质以及平行线的性质,解决问题的关键在于熟悉掌握知识要点,并且善于运用角与角之间的联系进行传递.(1)由AD∥BC,DE平分∠ADB,得∠ADC+∠BCD=180,∠BDC=∠BCD,得出∠1+∠2=90°;(2)由DE平分∠ADB,CD平分∠ABD,四边形ABCD中,AD∥BC,∠F=55°,得出∠ABC=∠ABD+∠DBC=∠ABD+∠ADB,即∠ABC=70°;(3)在△BMF中,根据角之间的关系∠BMF=180°﹣∠ABD﹣∠BFH,得∠GND=180°﹣∠AED﹣∠BFG,再根据角之间的关系得∠BAD= ![]() ﹣∠DBC,在综上得出答案.
﹣∠DBC,在综上得出答案.
【考点精析】本题主要考查了角的平分线和平行线的性质的相关知识点,需要掌握从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线;两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补才能正确解答此题.

【题目】一支原长为20cm的蜡烛,点燃后,其剩余长度y(cm)与燃烧时间x(min)之前的关系如表:
燃烧时间x(min) | 10 | 20 | 30 | 40 | 50 | … |
剩余长度y(cm) | 19 | 18 | 17 | 16 | 15 | … |
(1)表中反映的自变量是什么?因变量是什么?
(2)求出剩余长度y(cm)与燃烧时间x(min)之间的关系式;
(3)估计这支蜡烛最多可燃烧多少分钟?

