题目内容
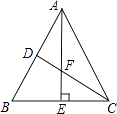
【题目】如图,在△ABC中,∠B=∠C,∠BAD=34°,且∠ADE=∠AED,则∠CDE=度. 
【答案】17
【解析】解:由三角形的外角性质得,∠ADC=∠B+∠BAD, ∠AED=∠C+∠CDE,
所以,∠ADE=∠ADC﹣∠CDE=∠B+∠BAD﹣∠CDE,
∵∠ADE=∠AED,
∴∠B+∠BAD﹣∠CDE=∠C+∠CDE,
∵∠B=∠C,
∴∠CDE= ![]() ∠BAD,
∠BAD,
∵∠BAD=34°,
∴∠CDE= ![]() ×34°=17°.
×34°=17°.
所以答案是:17°.
【考点精析】掌握三角形的内角和外角和三角形的外角是解答本题的根本,需要知道三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角;三角形一边与另一边的延长线组成的角,叫三角形的外角;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目