题目内容
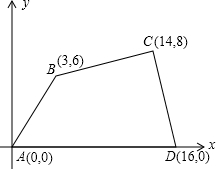 如图所示,在直角坐标系中,四边形ABCD各个顶点的坐标分别是A(0,0),B(3,6),C(14,8),D(16,0),确定这个四边形的面积.
如图所示,在直角坐标系中,四边形ABCD各个顶点的坐标分别是A(0,0),B(3,6),C(14,8),D(16,0),确定这个四边形的面积.
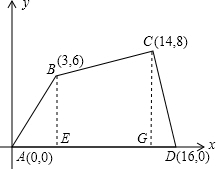
分析:分别过B、C作x轴的垂线,利用分割法求面积和即可.
解答:解:分别过B、C作x轴的垂线BE、CG,垂足为E,G.
所以SABCD=S△ABE+S梯形BEGC+S△CGD=
×3×6+
×(6+8)×11+
×2×8=94.
所以SABCD=S△ABE+S梯形BEGC+S△CGD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |

点评:主要考查了点的坐标的意义以及与图形相结合的具体运用.割补法是求面积问题的常用方法.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
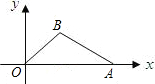 sin∠BOA=
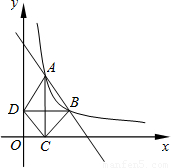
sin∠BOA=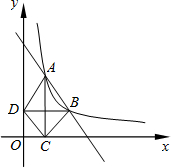 1.过点A作x轴垂线,垂足为C,过点B作y轴垂线,垂足为D,连接AD、DC、CB.
1.过点A作x轴垂线,垂足为C,过点B作y轴垂线,垂足为D,连接AD、DC、CB.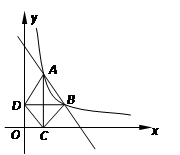

 的图象经过A(1,4),B(a,b),其中a>1.过点A作x轴垂线,垂足为C,过点B作y轴垂线,垂足为D,连接AD、DC、CB.
的图象经过A(1,4),B(a,b),其中a>1.过点A作x轴垂线,垂足为C,过点B作y轴垂线,垂足为D,连接AD、DC、CB.