题目内容
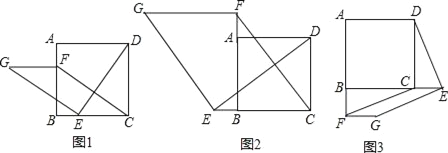
【题目】如图1,在正方形ABCD中,点E、F分别是边BC、AB上的点,且CE=BF,连接DE,过点E作EG⊥DE,使EG=DE,连接FG,FC.
(1)请判断:FG与CE的数量关系和位置关系;(不要求证明)
(2)如图2,若点E、F分别是CB、BA延长线上的点,其它条件不变,(1)中结论是否仍然成立?请给出判断并予以证明;
(3)如图3,若点E、F分别是BC、AB延长线上的点,其它条件不变,(1)中结论是否仍然成立?请直接写出你的判断.
【答案】(1)FG = CE, FG ∥ CE;
(2)仍然成立,证明见解析;
(3)FG = CE , FG ∥ CE仍然成立. 。
【解析】试题分析:(1)结论:FG=CE,FG∥CE.如图1中,设DE与CF交于点M,首先证明△CBF≌△DCE,推出DE⊥CF,再证明四边形EGFC是平行四边形即可.(2)结论仍然成立.如图2中,设DE与CF交于点M,首先证明△CBF≌△DCE,推出DE⊥CF,再证明四边形EGFC是平行四边形即可.(3)结论仍然成立.如图3中,设DE与FC的延长线交于点M,证明方法类似.
试题解析:(1)结论:FG=CE,FG∥CE.

理由:图1中,设DE与CF交于点M.
∵四边形ABCD是正方形,
∴BC=CD,∠ABC=∠DCE=90°,
在△CBF和△DCE中,
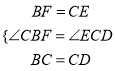 ,
,
∴△CBF≌△DCE,
∴∠BCF=∠CDE,CF=DE,
∵∠BCF+∠DCM=90°,
∴∠CDE+∠DCM=90°,
∴∠CMD=90°,
∴CF⊥DE,
∵GE⊥DE,
∴EG∥CF,
∵EG=DE,CF=DE,
∴EG=CF,
∴四边形EGFC是平行四边形。
∴GF=EC,
∴GF=EC,GF∥EC.
(2)结论仍然成立。
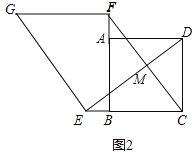
理由:如图2中,设DE与CF交于点M.
∵四边形ABCD是正方形,
∴BC=CD,∠ABC=∠DCE=90,
在△CBF和△DCE中,
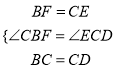 ,
,
∴△CBF≌△DCE,
∴∠BCF=∠CDE,CF=DE,
∵∠BCF+∠DCM=90°,
∴∠CDE+∠DCM=90°,
∴∠CMD=90°,
∴CF⊥DE,
∵GE⊥DE,
∴EG∥CF,
∵EG=DE,CF=DE,
∴EG=CF,
∴四边形EGFC是平行四边形。
∴GF=EC,
∴GF=EC,GF∥EC.
(3)结论仍然成立。

理由:如图3中,设DE与FC的延长线交于点M.
∵四边形ABCD是正方形,
∴BC=CD,∠ABC=∠DCE=90,
∴∠CBF=∠DCE=90
在△CBF和△DCE中,
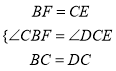 ,
,
∴△CBF≌△DCE,
∴∠BCF=∠CDE,CF=DE
∵∠BCF+∠DCM=90°,
∴∠CDE+∠DCM=90°,
∴∠CMD=90°,
∴CF⊥DE,
∵GE⊥DE,
∴EG∥CF,
∵EG=DE,CF=DE,
∴EG=CF,
∴四边形EGFC是平行四边形。
∴GF=EC,
∴GF=EC,GF∥EC.