题目内容
【题目】如图,在等腰△ABC中,∠A=80°,∠B和∠C的平分线相交于点O
(1)连接OA,求∠OAC的度数;
(2)求:∠BOC。
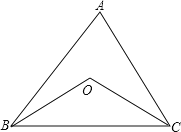
【答案】(1) 40°;(2) 130°
【解析】试题分析:(1)连接AO,利用等腰三角形的对称性即可求得∠OAC的度数;(2)利用三角形的内角和定理以及角平分线的定义求∠BOC与∠A的关系,再把∠A代入即可求∠BOC的度数.
试题解析:
(1)连接AO,
∵在等腰△ABC中,∠B和∠C的平分线相交于点O,
∴等腰△ABC关于线段AO所在的直线对称,
∵∠A=80°,
∴∠OAC=40°
(2)∵BO、CO分别平分∠ABC和∠ACB,
∴∠OBC= ∠ABC,∠OCB=∠ACB,
∴∠BOC=180°-(∠OBC+∠OCB)
=180°-( ∠ABC+∠ACB)
=180°- (∠ABC+∠ACB)
=180°- (180°-∠A)
=90°+∠A。
∴当∠A=80°时,
∠BOC=180° (∠B+∠C)=90°+∠A=130°。

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目