题目内容
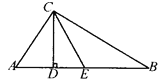
【题目】已知:如图,点C在线段AB上,以AC和BC为边在AB的同侧作正三角形△ACM和△BCN,连结AN、BM,分别交CM、CN于点P、Q.求证:PQ∥AB.
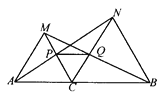
【答案】见解析
【解析】试题分析:首先证明△ACN≌△MCB可得∠ANC=∠MBC,再证明△PCN≌△QCB可得PC=QC,再有∠MCN=60°可得△PCQ是等边三角形,进而得到∠PQC=60°,可证明PQ∥AB.
试题解析:∵△ACM和△BCN都是正三角形,
∴∠ACM=∠BCN=60°,AC=CM,BC=CN.
∵点C在线段AB上,
∴∠ACM=∠BCN=∠MCN=60°.
∴∠ACM+∠MCN=∠BCN+∠MCN=120°.
即∠NCA=∠BCM=120°.
∵在△ACN和△MCB中,
 ,
,
∴△ACN≌△MCB(SAS),
∴∠ANC=∠MBC,
∵在△PCN和△QCB中,
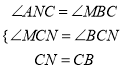 ,
,
∴△PCN≌△QCB(AAS),
∴PC=QC,
∵∠PCQ=60°,
∴△PCQ是等边三角形,
∴∠PQC=60°,
∴∠PQC=∠QCB,
∴PQ∥AB.

练习册系列答案
相关题目