题目内容
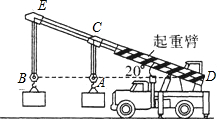
如图,水平面上放置一圆锥,在圆锥顶端斜靠着一根木棒(木棒的厚度可忽略不计),

小明为了探究这个问题,将此情景画在了草稿纸上(如图2正视图),运动过程:木棒顶端从A点开始沿圆锥的母线下滑,速度为θ1(木棒下滑为匀速),已知木棒与水平地面的夹角为θ,θ随木棒的下滑而不断减小,θ的最大值为30°,若木棒长为2
,问:当木棒顶端重A滑到B这个过程中,木棒末端的速度v′2是多少?

小明为了探究这个问题,将此情景画在了草稿纸上(如图2正视图),运动过程:木棒顶端从A点开始沿圆锥的母线下滑,速度为θ1(木棒下滑为匀速),已知木棒与水平地面的夹角为θ,θ随木棒的下滑而不断减小,θ的最大值为30°,若木棒长为2
| 3 |
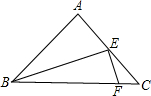
如图,作AE⊥BE,垂足为E,
由题意知,∠AGE=30°,∠ABE=60°,
∴∠AGE=∠GAB=30°,AB=GB,AE=AGsin30°=2
×
=
,
AB=GB=AE÷(sin60°)=
÷
=2,BE=ABcos60°=1,
当木棒顶端从点A移动到点B时,且是匀速移动,用的时间为t,移动的距离为AB=2,
则木棒的底端也从点G移动到点F,用的时间也为t,移动的距离FG=FB-GB=AG-AB=2
-2,
∴t=
=
,
∴vˊ=(
-1)v.

由题意知,∠AGE=30°,∠ABE=60°,
∴∠AGE=∠GAB=30°,AB=GB,AE=AGsin30°=2
| 3 |
| 1 |
| 2 |
| 3 |
AB=GB=AE÷(sin60°)=
| 3 |
| ||
| 2 |
当木棒顶端从点A移动到点B时,且是匀速移动,用的时间为t,移动的距离为AB=2,
则木棒的底端也从点G移动到点F,用的时间也为t,移动的距离FG=FB-GB=AG-AB=2
| 3 |
∴t=
2
| ||
| v′ |
| 2 |
| v |
∴vˊ=(
| 3 |


练习册系列答案
相关题目


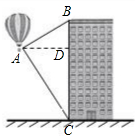 AD为66米.
AD为66米.