Question

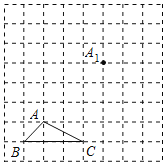
【题目】如图，正方形网格中，小正方形的边长为1．△ABC的顶点都在格点上．

（1）把△ABC沿BA方向平移后，点A移到点A1，在网格中画出平移后得到的△A1B1C1；

（2）把△A1B1C1绕点A1逆时针旋转90°，在网格中画出旋转后的△A1B2C2；

（3）在（2）的条件下，直接写出点C1至点C2的经过的路径长．

Answer 1

【答案】（1）见解析；（2）见解析；（3）π

【解析】

（1）利用点A和A1的位置确定平移的方向与距离，然后利用此平移规律画出B、C的对应点B1、C1；

（2）利用网格特点和旋转的性质画出B1、C1的对应点B2、C2即可；

（3）先利用勾股定理求出A1C1的长，再利用弧长公式计算．

解：（1）如图，△A1B1C1为所作；

（2）如图，△A1B2C2为所作；

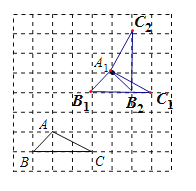
（3）∵A1C1=，

∴点C1至点C2的经过的路径长＝＝π．