题目内容
如图,在平面直角坐标系中,一次函数y=-2x的图像与反比例函数 的图像的一个交点为A(-1,n).
的图像的一个交点为A(-1,n).
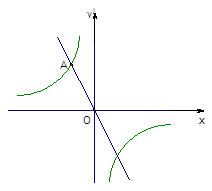
(1)求反比例函数 的解析式;
的解析式;
(2)若P是坐标轴上的一点,且满足PA=0A,直接写出P的坐标.
 的图像的一个交点为A(-1,n).
的图像的一个交点为A(-1,n).
(1)求反比例函数
 的解析式;
的解析式;(2)若P是坐标轴上的一点,且满足PA=0A,直接写出P的坐标.
(1)∵点A(﹣1,n)在一次函数y=﹣2x的图象上.
∴n=﹣2×(﹣1)=2
∴点A的坐标为(﹣1,2)
∵点A在反比例函数的图象上.
∴k=﹣2
∴反比例函数的解析式是y=﹣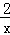 .
.
(2)∵A(﹣1,2),
∴OA=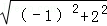 =
=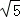 ,
,
∵点P在坐标轴上,
∴当点P在x轴上时设P(x,0),
∵PA=OA,
∴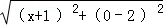 =
=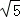 ,解得x=﹣2;
,解得x=﹣2;
当点P在y轴上时,设P(0,y),
∴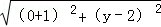 =
=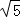 ,解得y=4;
,解得y=4;
当点P在坐标原点,则P(0,0).
∴点P的坐标为(﹣2,0)或(0,4)或(0,0).
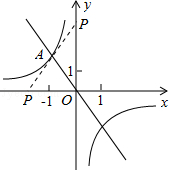
∴n=﹣2×(﹣1)=2
∴点A的坐标为(﹣1,2)
∵点A在反比例函数的图象上.
∴k=﹣2
∴反比例函数的解析式是y=﹣
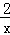 .
.(2)∵A(﹣1,2),
∴OA=
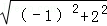 =
=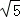 ,
,∵点P在坐标轴上,
∴当点P在x轴上时设P(x,0),
∵PA=OA,
∴
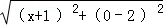 =
=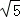 ,解得x=﹣2;
,解得x=﹣2;当点P在y轴上时,设P(0,y),
∴
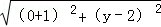 =
=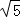 ,解得y=4;
,解得y=4;当点P在坐标原点,则P(0,0).
∴点P的坐标为(﹣2,0)或(0,4)或(0,0).
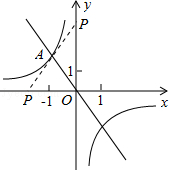
(1)把A的坐标代入函数解析式即可求得k的值,即可得到函数解析式;
(2)以A为圆心,以OA为半径的圆与坐标轴的交点就是P.
(2)以A为圆心,以OA为半径的圆与坐标轴的交点就是P.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
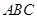 中,
中,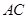 边的长为
边的长为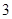 (
(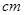 ),
),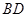 为
为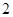 (
(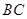 边的长为
边的长为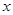 (
(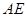 为
为 (
(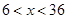 时
时 的图象交于点A(4,2),与x轴交于点B.
的图象交于点A(4,2),与x轴交于点B.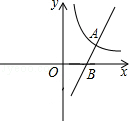
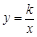 (x>0)图象于点C;连结OB交反比例函数
(x>0)图象于点C;连结OB交反比例函数
 的图象的对称轴有______条.
的图象的对称轴有______条. (x>0)的函数值随x的增大而
(x>0)的函数值随x的增大而 与反比例函数
与反比例函数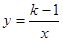 在同一坐标系中的图象不可能是
在同一坐标系中的图象不可能是
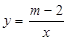 的图象在第二、四象限,则m的取值范围为
的图象在第二、四象限,则m的取值范围为