题目内容
【题目】如图,在正方形ABCD中,点E在AB边上,点F在BC边的延长线上,且AE=CF 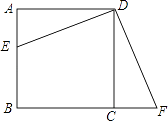
(1)求证:△AED≌△CFD;
(2)将△AED按逆时针方向至少旋转多少度才能与△CFD重合,旋转中心是什么?
【答案】
(1)解:∵四边形ABCD是正方形,
∴AD=CD,∠A=∠DCB=∠ADC=90°,
∴∠A=∠DCF=90°.
在△AED和△CFD中,
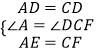 ,
,
∴△AED≌△CFD(SAS)
(2)解:∵∠ADC=90°,
∴△AED按逆时针方向至少旋转90度才能与△CFD重合,旋转中心是点D
【解析】(1)由正方形的性质就可以得出AD=CD,∠A=∠DCF=90°,再由SAS就可以得出结论;(2)由∠ADC=90°就可以得出△AED按逆时针方向至少旋转90度才能与△CFD重合,旋转中心是点D.
【考点精析】根据题目的已知条件,利用正方形的性质和旋转的性质的相关知识可以得到问题的答案,需要掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形;①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案【题目】当前,“校园手机”现象已经受到社会广泛关注,某数学兴趣小组对“是否赞成中学生带手机进校园”的问题进行了社会调查.小文将调查数据作出如下不完整的整理: 频数分布表
看法 | 频数 | 频率 |
赞成 | 5 | |
无所谓 | 0.1 | |
反对 | 40 | 0.8 |

(1)请求出共调查了多少人;并把小文整理的图表补充完整;
(2)小丽要将调查数据绘制成扇形统计图,则扇形图中“赞成”的圆心角是多少度?