题目内容
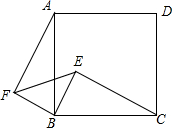 如图,已知四边形ABCD是正方形,E是正方形内一点,以BC为斜边作直角三角形BCE,又以BE为直角边作等腰直角三角形EBF,且∠EBF=90°,连接AF.
如图,已知四边形ABCD是正方形,E是正方形内一点,以BC为斜边作直角三角形BCE,又以BE为直角边作等腰直角三角形EBF,且∠EBF=90°,连接AF.(1)求证:AF=CE;
(2)求证:AF∥EB;
(3)若AB=5
| 3 |
| BF |
| CE |
| ||
| 3 |
分析:(1)根据正方形的性质和已知条件证明△FBA≌△EBC,即可得到AF=CE;
(2)由(1)知△FBA≌△EBC,所以∠FAB=∠ECB,再证明∠FAB=∠ABE,即可证明AF∥EB;
(3)设BE=
x,CE=3x,根据勾股定理 6x2+9x2=(5
)2,解方程求出x的值,再根据面积定值即可求出点E到BC的距离.
(2)由(1)知△FBA≌△EBC,所以∠FAB=∠ECB,再证明∠FAB=∠ABE,即可证明AF∥EB;
(3)设BE=
| 6 |
| 3 |
解答:证明:(1)∵四边形ABCD是正方形,
∴BA=BC,∠ABC=90°,
∵∠FBE=90°,
∴∠FBA+∠ABE=∠ABE+∠EBC=90°,
∴∠FBA=∠EBC,
∵在△FBA和△EBC中,
,
∴△FBA≌△EBC(SAS),
∴AF=CE;
(2)由(1)知△FBA≌△EBC,
∴∠FAB=∠ECB,
又∵∠EBC=∠ABE(都是∠EBC的余角),
∴∠FAB=∠ABE,
∴AF∥EB;
(3)∵
=
,
∴设BE=
x,CE=3x,
则 6x2+9x2=(5
)2
解得:x=
∴BE=
,CE=3
由面积相等得 BE•CE=BC•h,
解得 h=3
,
∴点E到BC的距离为 3
.
∴BA=BC,∠ABC=90°,
∵∠FBE=90°,
∴∠FBA+∠ABE=∠ABE+∠EBC=90°,

∴∠FBA=∠EBC,
∵在△FBA和△EBC中,
|
∴△FBA≌△EBC(SAS),
∴AF=CE;
(2)由(1)知△FBA≌△EBC,
∴∠FAB=∠ECB,
又∵∠EBC=∠ABE(都是∠EBC的余角),
∴∠FAB=∠ABE,
∴AF∥EB;
(3)∵
| BF |
| CE |
| ||
| 3 |
∴设BE=
| 6 |
则 6x2+9x2=(5
| 3 |
解得:x=
| 5 |
∴BE=
| 30 |
| 5 |
由面积相等得 BE•CE=BC•h,
解得 h=3
| 2 |
∴点E到BC的距离为 3
| 2 |
点评:本题考查了正方形的性质、全等三角形的判定和性质、平行线的判定以及勾股定理的运用,题目的综合性较强,难度中等.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
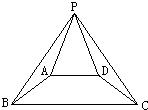 15、如图,已知四边形ABCD是等腰梯形,AB=DC,AD∥BC,PB=PC.求证:PA=PD.
15、如图,已知四边形ABCD是等腰梯形,AB=DC,AD∥BC,PB=PC.求证:PA=PD.
 的延长线分别交于点F、E,且
的延长线分别交于点F、E,且 (2013•梧州)如图,已知:AB∥CD,BE⊥AD,垂足为点E,CF⊥AD,垂足为点F,并且AE=DF.
(2013•梧州)如图,已知:AB∥CD,BE⊥AD,垂足为点E,CF⊥AD,垂足为点F,并且AE=DF.