题目内容
下列命题中:①如果两个三角形关于某条直线对称,那么这两个三角形全等;②若两图形关于某直线对称,则对称轴是对应点所连线段的垂直平分线;③等腰三角形底边垂直平分线上的任一点到两腰的距离相等;④一腰上的中线也是这条腰上的高的等腰三角形是等边三角形.其中正确命题的个数为
- A.1个
- B.2个
- C.3个
- D.4个
D
分析:根据轴对称的性质即可判断①②;根据等腰三角形性质求出MN平分∠CAB,根据角平分线性质求出,即可判断③;根据线段垂直平分线性质求出AB=BC,根据等边三角形判定判断即可.
解答:根据轴对称的性质得到:如果两个三角形关于某条直线对称,那么这两个三角形全等;∴①正确;
若两图形关于某直线对称,则对称轴是对应点所连线段的垂直平分线;∴②正确;
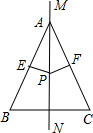
∵AB=AC,MN是BC的垂直平分线,
∴A在MN上,且AN平分∠CAB,
∵PE⊥AB,PF⊥AC,
∴PE=PF,∴③正确;
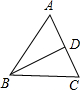
∵BD是△ABC的中线,BD⊥AC,
∴AB=BC,
∵AB=AC,
∴AC=BC=AB,
∴等腰△ABC是等边三角形,∴④正确;
故选D.
点评:本题考查了线段的垂直平分线性质,等腰三角形的性质,等边三角形的判定等知识点的运用,判断①②关键是理解性质,判断③④的关键是运用性质进行推理,题型较好,主要培养学生分析问题的能力.
分析:根据轴对称的性质即可判断①②;根据等腰三角形性质求出MN平分∠CAB,根据角平分线性质求出,即可判断③;根据线段垂直平分线性质求出AB=BC,根据等边三角形判定判断即可.
解答:根据轴对称的性质得到:如果两个三角形关于某条直线对称,那么这两个三角形全等;∴①正确;
若两图形关于某直线对称,则对称轴是对应点所连线段的垂直平分线;∴②正确;

∵AB=AC,MN是BC的垂直平分线,
∴A在MN上,且AN平分∠CAB,
∵PE⊥AB,PF⊥AC,
∴PE=PF,∴③正确;
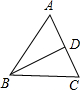
∵BD是△ABC的中线,BD⊥AC,
∴AB=BC,
∵AB=AC,
∴AC=BC=AB,
∴等腰△ABC是等边三角形,∴④正确;
故选D.
点评:本题考查了线段的垂直平分线性质,等腰三角形的性质,等边三角形的判定等知识点的运用,判断①②关键是理解性质,判断③④的关键是运用性质进行推理,题型较好,主要培养学生分析问题的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目