题目内容
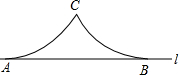 如图,A,B是直线l上的两点,且AB=2,两个半径相等的动圆分别与l相切于A,B点,C是这两个圆的公共点,则圆弧AC,CB与线段AB所围成图形面积S的最大值是
如图,A,B是直线l上的两点,且AB=2,两个半径相等的动圆分别与l相切于A,B点,C是这两个圆的公共点,则圆弧AC,CB与线段AB所围成图形面积S的最大值是分析:先判断出当r=1时两圆外切,再根据切线的性质可知四边形ABEF是长方形,由S最大=S长方形ABEF-S扇形ACF-S扇形BCE,即可得出结论.
解答: 解:∵AB=2,
解:∵AB=2,
∴当r=1时两圆正好外切,显然当两圆外切时圆弧AC,CB与线段AB所围成图形面积S的值最大,
∴过C作CD垂直AB,
过点C作EF∥AB,分别过点AB作AF⊥EF,BE⊥EF,则四边形ABEF是长方形,
则S最大=S长方形ABEF-S扇形ACF-S扇形BCE
=2×1-2×
π
=2-
.
 解:∵AB=2,
解:∵AB=2,∴当r=1时两圆正好外切,显然当两圆外切时圆弧AC,CB与线段AB所围成图形面积S的值最大,
∴过C作CD垂直AB,
过点C作EF∥AB,分别过点AB作AF⊥EF,BE⊥EF,则四边形ABEF是长方形,
则S最大=S长方形ABEF-S扇形ACF-S扇形BCE
=2×1-2×
| 1 |
| 4 |
=2-
| π |
| 2 |
点评:本题考查的是面积及等积变换,涉及到切线的性质、长方形的面积、扇形的面积公式,根据题意作出辅助线是解答此题的关键.

练习册系列答案
相关题目

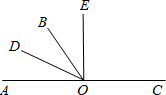 如图所示,O是直线AC上一点,OB是一条射线,OD平分∠AOB,OE在∠BOC内,∠BOE=
如图所示,O是直线AC上一点,OB是一条射线,OD平分∠AOB,OE在∠BOC内,∠BOE= 如图,A,B是直线l上两点,则图中有
如图,A,B是直线l上两点,则图中有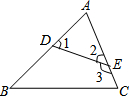 如图,∠
如图,∠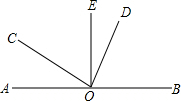 如图所示,O是直线AB上的点,∠AOC=40°,OD平分∠BOC.
如图所示,O是直线AB上的点,∠AOC=40°,OD平分∠BOC.