Question

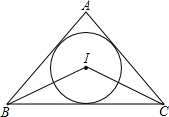
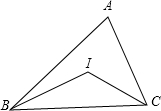
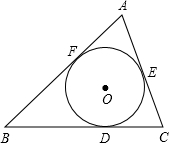
△ABC外切于⊙O，切点分别为点D、E、F，∠A=60°，BC=7，⊙O的半径为

3

．求：
（1）求BF+CE的值；
（2）求△ABC的周长．

Answer 1

（1）∵△ABC外切于⊙O，切点分别为点D、E、F，
∴BF=BD，CE=CD，
∴BF+CE=BD+CD=BC=7，
答：BF+CE的值是7．

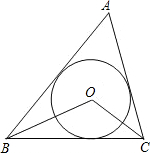
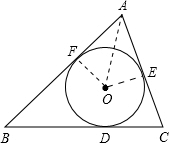
（2）连接OE、OF、OA，
∵△ABC外切于⊙O，切点分别为点D、E、F，
∴∠OEA=90°，∠OAE=

1

2

∠BAC=30°，
∴OA=2OE=2

3

，
由勾股定理得：AE=AF=

OA2-OE2

=

(2 3 )2-( 3 )2

=3，
∴△ABC的周长是AB+BC+AC=AF+AE+CE+BF+BC=7+7+3+3=20，
答：△ABC的周长是20．