题目内容
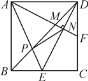
【题目】如图,正方形ABCD的边长为2,点E是BC的中点,AE与BD交于点P,F是CD上一点,连接AF分别交BD,DE于点M,N且AF⊥DE,连接PN,则以下结论中:①S△ABM=4S△FDM;②PN=![]() ;③tan∠EAF=
;③tan∠EAF=![]() ;④△PMN∽△DPE.正确的是________.(填序号)
;④△PMN∽△DPE.正确的是________.(填序号)
【答案】①②③
【解析】
先证ABM~FDM,利用相似三角形的性质即可判断①;过点P作PH⊥AN于点H,根据平行线分线段成比例定理,求出AP,AH的长,进一步得PH,HN的长,由勾股定理即可求出PN的长,即可判断②;分别求出EN,AN的长,即可判断③;证明∠DPN≠∠PDE,即可判断④.
∵正方形ABCD的边长为2,点E是BC的中点,
∴AB=BC=CD=AD=2,∠ABC=∠C=∠ADF=90°,CE=BE=1,
∵AF⊥DE,
∴∠DAF+∠ADN=∠ADN+∠CDE=90°,
∴∠DAF=∠CDE,
又∵AD=CD,∠ADF=∠DCE=90°,
∴ADFDCE(ASA),
∴DF=CE=1,
∵AB∥DF,
∴ABM~FDM,
∴![]() ,
,
∴S△ABM=4S△FDM,故①正确;
∵AB=CD,BE=CE,∠ABE=∠C=90°,
∴ABEDCE(SAS),
∴AE=DE=AF=![]() ,
,
∵![]() ,
,
∴DN=![]() ,
,
∴EN=DE-DN=![]() -
-![]() =
=![]() ,AN=
,AN=![]() ,
,
∴tan∠EAF=![]() ,故③正确;
,故③正确;
过点P作PH⊥AN于点H,
∵BE∥AD,
∴![]() ,
,
∴PA=![]() ,
,
∵tan∠EAF=![]() ,
,
∴sin∠EAF=![]() ,
,
∴PH=PAsin∠EAF=![]() ,
,
∵PH∥EN,
∴![]() ,
,
∴AH=![]() ,HN=AN-AH=
,HN=AN-AH=![]() ,
,
∴PN=![]() ,故②正确;
,故②正确;
∵PN≠DN,
∴∠DPN≠∠PDE,
∴△PMN与△DPE不相似,故④错误.
故答案是:①②③.

练习册系列答案
相关题目