题目内容
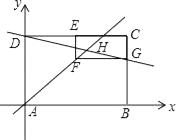
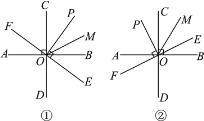
【题目】如图,已知O为直线AB上的一点,CD⊥AB于点O,PO⊥OE于点O,OM平分∠COE,点F在OE的反向延长线上.
(1)当OP在∠BOC内,OE在∠BOD内时,如图①所示,直接写出∠POM和∠COF之间的数量关系;
(2)当OP在∠AOC内且OE在∠BOC内时,如图②所示,试问(1)中∠POM和∠COF之间的数量关系是否发生变化?并说明理由.
【答案】(1)∠POM=![]() ∠COF,理由见解析;(2)∠POM=
∠COF,理由见解析;(2)∠POM=![]() ∠COF,理由见解析
∠COF,理由见解析
【解析】
(1)利用垂直的定义,CD⊥AB,PO⊥EO,等量代换得∠COP=∠BOE,利用角平分线的性质,得∠POM=![]() ∠POB=
∠POB=![]() (90°-∠POC),∠COF=90°-∠COP,得出结论;
(90°-∠POC),∠COF=90°-∠COP,得出结论;
(2)利用垂直的定义,同角的余角相等可得∠COP=∠AOF,可推出∠COP+∠COB=∠AOF+∠AOC,即∠BOP=∠COF,由对顶角相等得∠AOF=∠BOE=∠COP,利用角平分线的性质,得∠COP+∠COM=∠BOE+∠MOE,即∠POM=![]() ∠BOP,等量代换得出结论.
∠BOP,等量代换得出结论.
解:(1)∠POM=![]() ∠COF.
∠COF.
证明:∵CD⊥AB,
∴∠COP+∠BOP=90°,
∵OP⊥OE,
∴∠BOE+∠BOP=90°,
∴∠COP=∠BOE,
∵OM平分∠COE,
∴∠POM=∠MOB=![]() ∠POB=
∠POB=![]() (90°∠POC),
(90°∠POC),
∵∠COF=90°∠COP,
∴∠POM=![]() ∠COF;
∠COF;
(2)不发生变化.理由:∵CD⊥AB于点O,
∴∠AOP+∠COP=90°.
∵PO⊥OE于点O,
∴∠AOP+∠AOF=90°,
∴∠COP=∠AOF.
又∵∠AOC=∠COB=90°,
∴∠COP+∠COB=∠AOF+∠AOC,
即∠BOP=∠COF.
∵∠AOF=∠BOE,∴∠COP=∠BOE.
∵OM平分∠COE,∴∠COM=∠MOE,
∴∠COP+∠COM=∠BOE+∠MOE,
∴∠POM=![]() ∠BOP,
∠BOP,
∴∠POM=![]() ∠COF.
∠COF.
故答案为:(1)∠POM=![]() ∠COF,理由见解析;(2)∠POM=
∠COF,理由见解析;(2)∠POM=![]() ∠COF,理由见解析.
∠COF,理由见解析.

 金博士一点全通系列答案
金博士一点全通系列答案【题目】某公司招聘职员两名,对甲、乙、丙、丁四名候选人进行了笔试和面试,各项成绩满分均为100分,然后再按笔试占60%、面试占40%计算候选人的综合成绩(满分为100分).
他们的各项成绩如下表所示:
候选人 | 笔试成绩/分 | 面试成绩/分 |
甲 | 90 | 88 |
乙 | 84 | 92 |
丙 | x | 90 |
丁 | 88 | 86 |
(1)直接写出这四名候选人面试成绩的中位数;
(2)现得知候选人丙的综合成绩为87.6分,求表中x的值;
(3)求出其余三名候选人的综合成绩,并以综合成绩排序确定所要招聘的前两名的人选.
【题目】下表是橘子的销售额随橘子卖出质量的变化表:
质量/千克 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | … |
销售额/元 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | … |
(1)这个表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)当橘子卖出5千克时,销售额是_______元.
(3)如果用![]() 表示橘子卖出的质量,
表示橘子卖出的质量,![]() 表示销售额,按表中给出的关系,
表示销售额,按表中给出的关系,![]() 与
与![]() 之间的关系式为______.
之间的关系式为______.
(4)当橘子的销售额是100元时,共卖出多少千克橘子?